题目内容
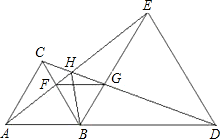 如图所示,已知△ABC与△BDE都是等到边三角形.下列结论:①AE=CD;②BF=BG;③BH⊥FG;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD;⑦△ABF≌△CGB;⑧△EFB≌△GBD,其中正确的有
如图所示,已知△ABC与△BDE都是等到边三角形.下列结论:①AE=CD;②BF=BG;③BH⊥FG;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD;⑦△ABF≌△CGB;⑧△EFB≌△GBD,其中正确的有
- A.4个
- B.5个
- C.6个
- D.7个
D
分析:由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
解答:∵△ABC与△BDE为等边三角形,∴AB=BC,BD=BE,
又∠ABE=∠CBD,
∴△ABE≌△CBD,∴AE=CD,∠BDC=∠AEB,
又∠DBG=∠FBE=60°,
∴△BGD≌△BFE,∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
∴△ABF≌△CGB,∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∴题中①②④⑤⑥⑦⑧正确,而③不正确.
故此题选D.
点评:本题主要考查了等边三角形的性质及全等三角形的判定及性质问题,能够熟练掌握.
分析:由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
解答:∵△ABC与△BDE为等边三角形,∴AB=BC,BD=BE,
又∠ABE=∠CBD,
∴△ABE≌△CBD,∴AE=CD,∠BDC=∠AEB,
又∠DBG=∠FBE=60°,
∴△BGD≌△BFE,∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
∴△ABF≌△CGB,∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∴题中①②④⑤⑥⑦⑧正确,而③不正确.
故此题选D.
点评:本题主要考查了等边三角形的性质及全等三角形的判定及性质问题,能够熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
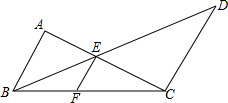 如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.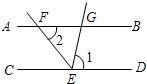 5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
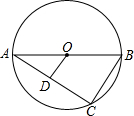 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.
如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.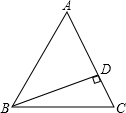 如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.
如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.