题目内容
【题目】如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
(1)用直尺画出该圆弧所在圆的圆心M的位置;
(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A、B、C的抛物线上;
(3)在(2)的条件下,求证:直线CD是⊙M的切线.
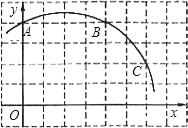
【答案】(1)画图参见解析;(2)不在;(3)证明参见解析.
【解析】
试题分析:(1)利用“两弦垂直平分线的交点为圆心”可确定圆心位置;(2)先根据A、B、C三点坐标,用待定系数法求出抛物线的解析式,然后将D点坐标代入抛物线的解析式中,即可判断出点D是否在抛物线的图象上;(3)由于C在⊙M上,如果CD与⊙M相切,那么C点必为切点;因此可连接MC,证MC是否与CD垂直即可.可根据C、M、D三点坐标,分别表示出△CMD三边的长,然后用勾股定理来判断∠MCD是否为直角.
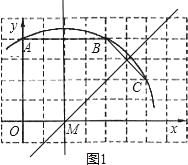
试题解析:(1)如下图,连接AB,BC,作线段AB,BC的垂直平分线,两线的交点M即为所求;(2)由A(0,4),可得小正方形的边长为1,从而B(4,4)、C(6,2),设经过点A、B、C的抛物线的解析式为y=ax2+bx+4
依题意![]() ,解得
,解得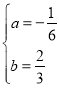 ,所以经过点A、B、C的抛物线的解析式为y=﹣
,所以经过点A、B、C的抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4,把点D(7,0)的横坐标x=7代入上述解析式,得y=-
x+4,把点D(7,0)的横坐标x=7代入上述解析式,得y=-![]() ×49+
×49+![]() ×7+4=
×7+4=![]() ≠0,所以点D不在经过A、B、C的抛物线上;(3)如图,设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD
≠0,所以点D不在经过A、B、C的抛物线上;(3)如图,设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD
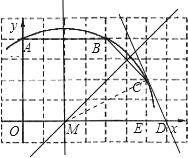
由图可知:CE=2,ME=4,ED=1,MD=5,在Rt△CEM中,∠CEM=90°,∴MC2=ME2+CE2=42+22=20,在Rt△CED中,∠CED=90°,∴CD2=ED2+CE2=12+22=5,∴MD2=MC2+CD2,∴∠MCD=90°,∵MC为半径,∴直线CD是⊙M的切线.

 阅读快车系列答案
阅读快车系列答案【题目】某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵) | 4 | 5 | 6 | 8 | 10 |
人数 | 30 | 22 | 25 | 15 | 8 |
则这100名同学平均每人植树棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是棵.