题目内容
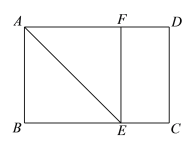
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,过E作EF⊥AD于F.
(1)求证:四边形ABEF是正方形;
(2)连接BF交AE于点O,连接DO,若CD=2,CE=1,求OD的长.
【答案】(1)证明见解析;(2)OD的长为![]() .
.
【解析】
(1)先根据矩形的判定可得出四边形ABEF是矩形,再根据角平分线的性质可得![]() ,然后根据正方形的判定即可得证;
,然后根据正方形的判定即可得证;
(2)如图(见解析),过点O作![]() 于点G,先根据正方形的性质得出点O为AE的中点,再根据中位线定理可得
于点G,先根据正方形的性质得出点O为AE的中点,再根据中位线定理可得![]() 的长,从而可得DG的长,然后利用勾股定理求解即可.
的长,从而可得DG的长,然后利用勾股定理求解即可.
(1)![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]()
![]()
![]()
![]() 四边形ABEF是矩形
四边形ABEF是矩形
又![]() 平分
平分![]()
![]() (角平分线的性质)
(角平分线的性质)
![]() 矩形ABEF是正方形
矩形ABEF是正方形
即四边形ABEF是正方形;
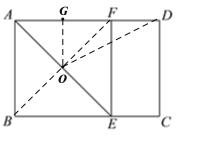
(2)如图,过点O作![]() 于点G,则
于点G,则![]()
同(1)可得:四边形CDFE是矩形
![]()
由(1)可知,四边形ABEF是正方形
![]() ,点O是对角线AE的中点
,点O是对角线AE的中点
![]()
![]() OG是
OG是![]() 的中位线
的中位线
![]() ,点G是AF的中点
,点G是AF的中点
![]()
![]()
在![]() 中,
中,![]()
故OD的长为![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
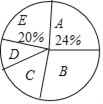
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?