Question

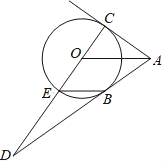
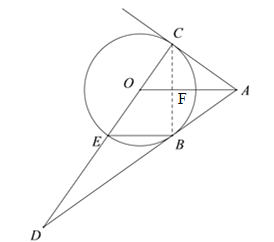
【题目】如图，AB，AC是⊙O的两条切线，B，C为切点，连接CO并延长交AB于点D，交⊙O于点E，连接BE，连接AO．

（1）求证：AO∥BE；

（2）若DE＝2，tan∠BEO＝，求DO的长．

Answer 1

【答案】(1))证明见解析；(2)DO=3.

【解析】

（1）由切线长定理得到OA⊥BC，再由直径所对的圆周角等于90°，即可得到结论；

（2）由平行线的性质得到∠BEO=∠AOC，设OC=r，解Rt△AOC，得到AC，OA，cos∠AOC的值，从而得到EB的值．再由△DBE∽△DAO得到对应边成比例，即可得到结论．

(1)连结BC．

∵AB，AC是⊙O的两条切线，B，C为切点，∴AB=AC，OA平分∠BAC，∴OA⊥BC，∴∠CFO=90°．

∵CE是⊙O的直径，∴∠CBE=90°，∴∠CFO=∠CBE，∴ OA∥BE．

(2)∵OA∥BE，∴∠BEO=∠AOC．

∵tan∠BEO=，∴tan∠AOC=．

在Rt△AOC中，设OC=r，则AC=r，OA=r ，∴cos∠AOC=，∴cos∠BEC= cos∠AOC =，∴EB=r．

∵BE∥OA，∴△DBE∽△DAO，∴，∴，∴DO=3．