题目内容
【题目】问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题
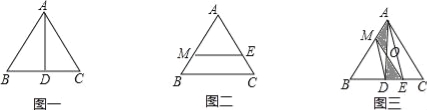
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
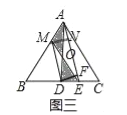
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE.
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
【答案】(1)AD=![]() ;(2)ME=
;(2)ME=![]() ;(3)详见解析;(3)
;(3)详见解析;(3)![]() ≤l≤
≤l≤![]() .
.
【解析】
试题分析:(1)根据等腰三角形三线合一即可证明,利用直角三角形30°性质,即可求出AD.(2)根据相似三角形性质面积比等于相似比的平方,即可解决问题.(3)如图三中,作MN⊥AE于N,DF⊥AE于F,先证明MN=DF,推出四边形MNFD是平行四边形即可.
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,求出EM,利用不等式性质证明ME≥![]() 即可解决问题.
即可解决问题.
试题解析:(1)如图一中,
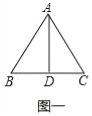
∵AB=AC=BC=2,AD⊥BC,
∴BD=DC,
∴S△ABD=S△ADC,
∴线段AD是△ABC的面径.
∵∠B=60°,
∴sin60°=![]() ,
,
∴![]() ,
,
∴AD=![]() .
.
(2)如图二中,
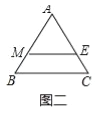
∵ME∥BC,且ME是△ABC的一条面径,
∴△AME∽△ABC,![]() =
=![]() ,
,
∴![]() ,
,
∴ME=![]() .
.
(3)如图三中,作MN⊥AE于N,DF⊥AE于F.
∵S△MOA=S△DOE,
∴S△AEM=S△AED,
∴![]() AEMN=
AEMN=![]() AEDF,
AEDF,
∴MN=DF,
∵MN∥DF,
∴四边形MNFD是平行四边形,
∴DM∥AE.
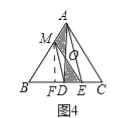
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,
∵DM∥AE,
∴![]() ,
,
∴![]() ,
,
∴xy=2,
在RT△MBF中,∵∠MFB=90°,∠B=60°,BM=x,
∴BF=![]() x,MF=
x,MF=![]() x,
x,
∴ME=![]()
∴ME≥![]() ,
,
∵ME是等边三角形面径,AD也是等边三角形面积径,
∴等边三角形ABC的面径长l的取值范围![]() ≤l≤
≤l≤![]() .
.