Question

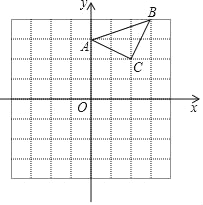
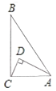
【题目】直角△ABC中，∠ACB=90°，AC=3cm，BC=4cm，AB=5cm，如果AD平分∠BAC，且ADCD，那么点D到AB的距离为 ______cm.

Answer 1

【答案】

【解析】

延长AD交BC于点F，过点F作FG⊥AB，过点D作DE⊥BC于E，由角平分线的性质定理则CF=FG，则△ACF≌△AGF，得到AG=AC=3，在Rt△BFG中，设FG=x，则BF=4x，BG=2，由勾股定理求出FG=CF=，然后利用勾股定理，求出AF的长度，利用面积法求出CD的长度，利用勾股定理求出AD的长度，再利用面积法求出DE的长度，即可得到点D到AB的距离.

解：如图，延长AD交BC于点F，过点F作FG⊥AB，过点D作DE⊥BC于E，

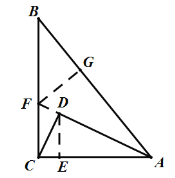
∵AD平分∠BAC，FG⊥AB，∠ACB=90°，

∴FC=FG，

∵∠ACB=∠AGF=90°，∠CAF=∠GAF，AF=AF，

∴△ACF≌△AGF，

∴AC=AG=3，

在Rt△BFG中，设FG=x，则BF=4x，BG=2，

由勾股定理，得：，

解得：，

∴CF=FG=.

在Rt△ACF中，由勾股定理，得：

；

∵，

即，

∴，

在Rt△ACD中，由勾股定理，得：

；

∵，

即，

解得：；

∵AD是角平分线，

∴点D到AB的距离为：.

故答案为：.