Question

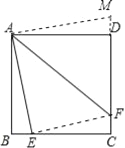
【题目】如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+DF与EF的关系是______．

Answer 1

【答案】BE+DF=EF

【解析】如图,延长CD到M,使DM=BE,

连接AM,EF,

∵四边形ABCD为正方形,

∴∠B=∠ADC=90°,AB=AD,

在△ABE与△ADM中,

,

∴△ABE≌△ADM（SAS）,

∴∠BAE=∠DAM,AE=AM,

∴∠BAE+∠DAF=∠DAM+∠DAF=∠MAF,

∵∠EAF=45°,

∴∠EAF=∠MAF=45°,

在△EAF与△MAF中,

，

∴△EAF≌△MAF（SAS）,

∴MF=EF,而MF=MD+DF=BE+DF,

∴BE+DF=EF,

故答案为BE+DF=EF.