题目内容
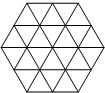 边长为2的正六边形,被三组平行线划分成如图所示的小正三角形,从图中任意选定一个正三角形,则选定的正三角形边长恰好是2的概率是
边长为2的正六边形,被三组平行线划分成如图所示的小正三角形,从图中任意选定一个正三角形,则选定的正三角形边长恰好是2的概率是
- A.

- B.
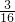
- C.
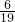
- D.

C
分析:分类计算:正六边形的边长为2,分别计算出边长为1的正三角形的个数个,边长为3的正三角形的个数,边长为2的正三角形的个数,然后相加即可得出正三角形总个数,进而得出正三角形边长恰好是2的概率.
解答:正六边形的边长为2,
那么边长为1的正三角形的有24个,边长为2的正三角形有12个,边长为3的正三角形的有2个,
共计38个,故选定的正三角形边长恰好是2的概率是: =
=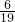 .
.
故选C.
点评:此题主要考查了等边三角形的性质以及概率求,根据正三角形性质得出正三角形总个数是解题关键.
分析:分类计算:正六边形的边长为2,分别计算出边长为1的正三角形的个数个,边长为3的正三角形的个数,边长为2的正三角形的个数,然后相加即可得出正三角形总个数,进而得出正三角形边长恰好是2的概率.
解答:正六边形的边长为2,
那么边长为1的正三角形的有24个,边长为2的正三角形有12个,边长为3的正三角形的有2个,
共计38个,故选定的正三角形边长恰好是2的概率是:
 =
=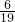 .
.故选C.
点评:此题主要考查了等边三角形的性质以及概率求,根据正三角形性质得出正三角形总个数是解题关键.

练习册系列答案
相关题目
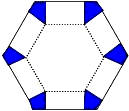 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
 如图,边长为1的正六边形在足够长的桌面上滚动(没有滑动)一周,则它的中心O点所经过的路径长为( )
如图,边长为1的正六边形在足够长的桌面上滚动(没有滑动)一周,则它的中心O点所经过的路径长为( )