题目内容
若一元二次方程x2-2x-k=0无实数根,则二次函数y=x2+(k+1)x+k的图象最低点在第 ________象限.
四
分析:根据一元二次方程x2-2x-k=0无实数根,得到k<-1,再求出二次函数y=x2+(k+1)x+k的顶点坐标,根据k<-1,判断出正负,最后根据象限点的特点即可填出答案.
解答:∵一元二次方程x2-2x-k=0无实数根,
∴b2-4ac=4+4k<0,
即k<-1,
已知二次函数y=x2+(k+1)x+k,
- =-
=-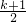 >0,
>0,
 =
= =-
=- <0,
<0,
∴图象在第四象限.
故答案为:四.
点评:本题考查了一元二次方程的判别式,二次函数的顶点坐标,平面直角坐标系的象限的点的特点等知识点,确定k的范围,进一步判断出顶点的横、纵坐标的正负是解此题的关键.
分析:根据一元二次方程x2-2x-k=0无实数根,得到k<-1,再求出二次函数y=x2+(k+1)x+k的顶点坐标,根据k<-1,判断出正负,最后根据象限点的特点即可填出答案.
解答:∵一元二次方程x2-2x-k=0无实数根,
∴b2-4ac=4+4k<0,
即k<-1,
已知二次函数y=x2+(k+1)x+k,
-
 =-
=-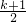 >0,
>0, =
= =-
=- <0,
<0,∴图象在第四象限.
故答案为:四.
点评:本题考查了一元二次方程的判别式,二次函数的顶点坐标,平面直角坐标系的象限的点的特点等知识点,确定k的范围,进一步判断出顶点的横、纵坐标的正负是解此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
若一元二次方程x2-x+m=0有两个不相等的实数根x1、x2,且满足
+
=-2,则m的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |