题目内容
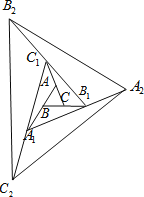
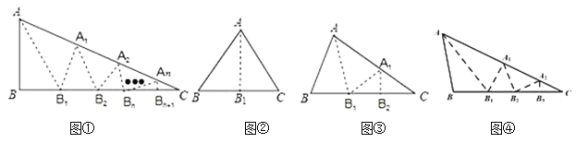
【题目】.如图①,ABC中,沿BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿B1A1C的平分线A1B2折叠,剪掉重叠部分;……将余下部分沿BnAnC(n为正整数)的平分线AnBn1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次点Bn与点C恰好重合,我们就称BAC是ABC的好角.
小丽展示了确定BAC是ABC的好角的两种情形.
情形一:如图②,沿等腰三角形ABC顶角BAC是平分线AB1折叠,点B与点C重合;
情形二:如图③,沿ABC的BAC的平分线AB1折叠,剪掉重叠部分;将余下的部分沿B1A1C的平分线A1B2折叠,此时点B1与点C重合.
(探究发现)
⑴如图③,ABC中,B2C,经过两次折叠,BAC是不是ABC的好角? .(填:“是”或“不是”)
⑵归纳猜想:(i)如图④,小丽经过三次折叠发现了BAC是ABC的好角,请探究B与C(BC)之间的等量关系,并说明理由.
(ii)根据以上内容猜想:若经过n(n为正整数)次折叠BAC是ABC的好角,则B与C(BC)之间的等量关系为 .(直接写出结论)
⑶小丽找到一个三角形,三个角分别为15,60,105,发现60和105的两个角都是此三角形的好角,请你完成,如果一个三角形的最小角是10,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
【答案】(1)是;
(2)∠B=3∠C;∠B=n∠C;
(3)60°,105°;
(4)10°,160°.
【解析】
(1)仔细分析题意根据折叠的性质及“好角”的定义即可作出判断;
(2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的∠A2B2C=∠C,由∠ABB1=∠AA1B1,∠AA1B1=∠A1B1C+∠C,又∠A1B1C=∠A1A2B2,∠A1A2B2=∠A2B2C+∠C,∠ABB1=∠A1B1C+∠C=∠A2B2C+∠C+∠C=3∠C,由此即可求得结果;
(3)根据好角的定义即可得出结果;
(4)根据好角的定义进行推理计算,即可得出结果.
解:(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是△ABC的好角;
理由如下:小丽展示的情形二中,
∵沿∠BAC的平分线AB1折叠,
∴∠B=∠AA1B1;
又∵将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合,
∴∠A1B1C=∠C;
∵∠AA1B1=∠C+∠A1B1C(外角定理),
∴∠B=2∠C;
故答案为:是;
(2)∠B=3∠C;
在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分,将余下部分沿∠B2A2C的平分线A2B3折叠,点B2与点C重合,则∠BAC是△ABC的好角.
理由如下:∵根据折叠的性质知,∠B=∠AA1B1,∠C=∠A2B2C,∠A1B1C=∠A1A2B2,
∴根据三角形的外角定理知,∠A1A2B2=∠C+∠A2B2C=2∠C;
∵根据四边形的外角定理知,∠BAC+∠B+∠AA1B1-∠A1B1C=∠BAC+2∠B-2C=180°,
根据三角形ABC的内角和定理知,∠BAC+∠B+∠C=180°,
∴∠B=3∠C;
由小丽展示的情形一知,当∠B=∠C时,∠BAC是△ABC的好角;
由小丽展示的情形二知,当∠B=2∠C时,∠BAC是△ABC的好角;
由小丽展示的情形三知,当∠B=3∠C时,∠BAC是△ABC的好角;
故若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为∠B=n∠C;
故答案为:∠B=3∠C;∠B=n∠C;
(3)由前边可以知道∠B和∠C有倍数关系,∠A是好角
所以60°=4×15°,60和15有倍数关系,105°应该是好角
105°=7×15°,105和15有倍数关系,60°应该是好角
故答案为:60°,105°;
(4)10°,160°;由(2)知,∠B=n∠C,∠BAC是△ABC的好角,
因为最小角是10°是△ABC的好角,
根据好角定义,则可设另两角分别为10m°,10mn°(其中m、n都是正整数).
由题意,得10m+10mn+10=180,所以m(n+1)=17.
因为m、n都是正整数,所以m与n+1是17的整数因子,
因此有:m=1,n+1=17;
所以m=1,n=16;
所以10m=10°,10mn=160°;
所以该三角形的另外两个角的度数分别为:10°,160°;
故答案为:10°,160°.

 科学实验活动册系列答案
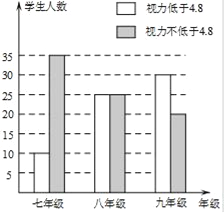
科学实验活动册系列答案【题目】2018年5月12日是我国第十个全国防灾减灾日,也是汶川地震十周年.为了弘扬防灾减灾文化,普及防灾减灾知识和技能,郑州W中学通过学校安全教育平台号召全校学生进行学习,并对学生学习成果进行了随机抽取,现对部分学生成绩(x为整数,满分100分)进行统计.绘制了如图尚不完整的统计图表:
调查结果统计表
组别 | 分数段 | 频数 |
A | 50≤x<60 | a |
B | 60≤x<70 | 80 |
C | 70≤x<80 | 100 |
D | 80≤x<90 | 150 |
E | 90≤x<100 | 120 |
合计 | b |
根据以上信息解答下列问题:
(1)填空:a= ,b= ;
(2)扇形统计图中,m的值为 ,“D”所对应的圆心角的度数是 度;
(3)本次调查测试成绩的中位数落在 组内;
(4)若参加学习的同学共有2000人,请你估计成绩在90分及以上的同学大约有多少人?