题目内容
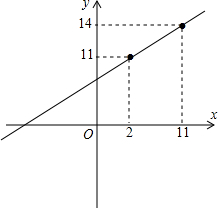
在平面上具有整数坐标的点称为整点.若一线段的端点分别为(2,11),(11,14),则在此线段上(包括端点)的整点共有( )
| A.3个 | B.4个 | C.6个 | D.8个 |
设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),则
,
解得,
,
∴所求的线段所在的直线方程为y=
x+
;
①当y=12时,x=5,即整点(5,12)在该线段上;
②当y=13时,x=8,即整点(8,13)在该线段上;
又∵端点(2,11)、(11,14)也是整点,
∴在此线段上(包括端点)的整点共有4个;
故选B.
|
解得,
|
∴所求的线段所在的直线方程为y=
| 1 |
| 3 |
| 31 |
| 3 |
①当y=12时,x=5,即整点(5,12)在该线段上;
②当y=13时,x=8,即整点(8,13)在该线段上;
又∵端点(2,11)、(11,14)也是整点,
∴在此线段上(包括端点)的整点共有4个;
故选B.


练习册系列答案
相关题目