题目内容
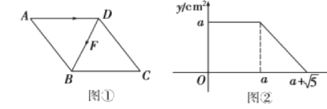
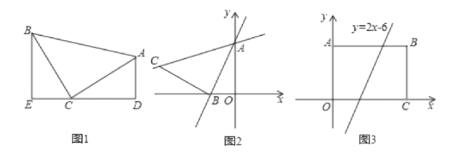
【题目】(1)模型建立，如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于D，过B作BE⊥ED于E.求证：△BEC≌△CDA；
(2)模型应用：
①已知直线y＝
x＋3与y轴交于A点，与x轴交于B点，将线段AB绕点B逆时针旋转90度，得到线段BC，过点A，C作直线.求直线AC的解析式；
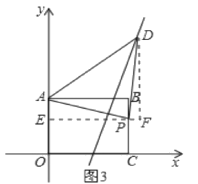
②如图3，矩形ABCO，O为坐标原点，B的坐标为(8，6)，A，C分别在坐标轴上，P是线段BC上动点，已知点D在第一象限，且是直线y＝2x－6上的一点，若△APD是不以A为直角顶点的等腰直角三角形，请直接写出所有符合条件的点D的坐标.
【答案】（1）见解析（2）y=
x+4（3）(4,2)或(
)或(
).
【解析】
（1）由条件可求得∠EBC=∠ACD，利用AAS可证明△BEC≌△CDA；
（2）由直线解析式可求得A、B的坐标，利用模型结论可得CE=BO，BE=AO，从而可求得C点坐标，利用待定系数法可求得直线AC的解析式；
（3）分三种情况考虑：如图2所示，当∠ADP=90°时，AD=PD，设D点坐标为（x，2x-6），利用三角形全等得到x+6-（2x-6）=8，得x=4，易得D点坐标；如图3所示，当∠APD=90°时，AP=PD，设点P的坐标为（8，m），表示出D点坐标为（14-m，m+8），列出关于m的方程，求出m的值，即可确定出D点坐标；如图4所示，当∠ADP=90°时，AD=PD时，同理求出D的坐标．
(1)∵∠ACB=90，
∴∠EBC+∠BCE=∠BCE+∠ACD=90，
∴∠EBC=∠ACD，
在△BEC和△CDA中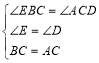
，
∴△BEC≌△CDA(AAS)；
(2)如图1,
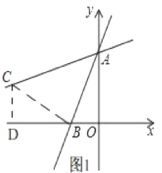
过点B作BC⊥AB交直线l
于C过C作CD⊥x轴于点D，
在y=
x+4中，令y=0可求得x=3，令x=0可求得y=4，
∴OA=4，OB=3，
同(1)可证得△CDB≌△BAO，
∴CD=BO=3，BD=AO=4，
∴OD=4+3=7，
∴C(7,3),且A(0,4)，
设直线AC解析式为y=kx+4,把C点坐标代入可得7k+4=3,解得k=，
∴直线AC解析式为y=x+4；
(3)如图2,
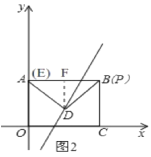
当∠ADP=90时，AD=PD，
过点P作PE⊥OA于E，过点D作DF⊥PE于F，
∴点E与点A重合,∴DF=
AB=4
设D点坐标为(x,2x6),6(2x6)=4，得x=4，
易得D点坐标(4,2)；
如图3,当∠APD=90°时，AP=PD，
过点P作PE⊥OA于E，过点D作DF⊥PE于F，
设点P的坐标为(8,m),易证,△APE≌△PDF，
∴PF=AE=6m，DF=PE=8，
∴D点坐标为(1m,m+8)，
∴m+8=2(14m)6,得m=
,
∴D点坐标()；
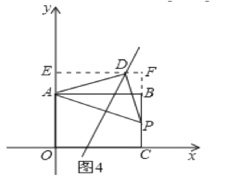
如图4,当∠ADP=90°时,AD=PD时,同理得D点坐标()，
综上可知满足条件的点D的坐标分别为(4,2)或()或().
