题目内容
【题目】阅读下列材料:
我们给出如下定义:数轴上给定两点![]() ,
,![]() 以及一条线段
以及一条线段![]() ,若线段
,若线段![]() 的中点
的中点![]() 在线段
在线段![]() 上(点
上(点![]() 可以与点
可以与点![]() 或
或![]() 重合),则称点
重合),则称点![]() 与点
与点![]() 关于线段
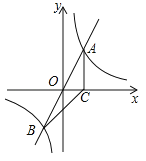
关于线段![]() 径向对称.下图为点
径向对称.下图为点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称的示意图.
径向对称的示意图.

解答下列问题:
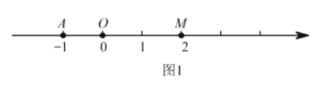
如图1,在数轴上,点![]() 为原点,点
为原点,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
(1)①点![]() ,
,![]() ,
,![]() 分别表示的数为-3,
分别表示的数为-3,![]() ,3,在
,3,在![]() ,
,![]() ,
,![]() 三点中, 与点
三点中, 与点![]() 关于线段
关于线段![]() 径向对称;
径向对称;
②点![]() 表示的数为
表示的数为![]() ,若点
,若点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称,则
径向对称,则![]() 的取值范围是 ;
的取值范围是 ;
(2)在数轴上,点![]() ,
,![]() ,
,![]() 表示的数分别是-5,-4,-3,当点
表示的数分别是-5,-4,-3,当点![]() 以每秒1个单位长度的速度向正半轴方向移动时,线段
以每秒1个单位长度的速度向正半轴方向移动时,线段![]() 同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为
同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为![]() (
(![]() )秒,问
)秒,问![]() 为何值时,线段
为何值时,线段![]() 上至少存在一点与点
上至少存在一点与点![]() 关于线段
关于线段![]() 径向对称.
径向对称.
【答案】(1)①点C和点D;②1≤x≤5;(2)![]()
【解析】
(1)根据题干中给出的径向对称的定义,进行验证解答即可;
(2)根据题干中给出的径向对称的定义,列出点x与点A中点的取值范围,即可求出答案;
(3)用含t的代数式分别表示出点H,K,L和线段HK与线段HL的中点列式计算即可.
解:(1)①与点A点关于线段![]() 径向对称需要满足:这个点与A点的中点在线段OM上,点B表示的数是-3,与点A表示的-1的中点是-2,不在线段OM上,所以点B不是;点C表示的数
径向对称需要满足:这个点与A点的中点在线段OM上,点B表示的数是-3,与点A表示的-1的中点是-2,不在线段OM上,所以点B不是;点C表示的数![]() ,与点A表示的-1的中点是
,与点A表示的-1的中点是![]() ,在线段OM上,所以点C是;点D表示的3与点A表示的-1的中点是1,在线段OM上,所以点D是;
,在线段OM上,所以点C是;点D表示的3与点A表示的-1的中点是1,在线段OM上,所以点D是;
综上,答案为点C,点D;
②
结合数轴可知当点x与点A的中点落在点O与点M之间时(包括端点O与M)符合题意,即![]() ,解得
,解得![]() ,故答案为
,故答案为![]() ;
;
(2)解:移动时间t(t>0)秒时,点H,K,L表示的数分别是-5+t,-4+3t,-3+3t,
此时,线段HK的中点设为R1,表示的数为![]() ,
,
线段HL的中点设为R2,表示的数为![]() ,
,

当线段R1 R2,在线段OM上运动时,线段KL上至少存在一点与点H关于线段OM径向对称,
当R2经过点O时,2t-4=0时,t=2,
当R1经过点M时,![]() 时,
时,![]() ,
,
所以当![]() 时,线段R1 R2在OM上运动,
时,线段R1 R2在OM上运动,
所以当![]() 时,线段KL上至少存在一点与点H关于线段OM径向对称.
时,线段KL上至少存在一点与点H关于线段OM径向对称.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案