题目内容
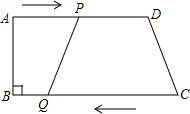 在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
分析:(1)设经过ts时,四边形PQCD是平行四边形,根据DP=CQ,代入后求出即可;
(2)设经过ts时,四边形PQBA是矩形,根据AP=BQ,代入后求出即可.
(2)设经过ts时,四边形PQBA是矩形,根据AP=BQ,代入后求出即可.
解答:解:(1)设经过ts时,四边形PQCD是平行四边形,
∵AP=t,CQ=3t,DP=24-t,
∴DP=CQ,
∴24-t=3t,
t=6,
即经过6s时,四边形PQCD是平行四边形;
(2)设经过ts时,四边形PQBA是矩形,
∵AP=t,CQ=3t,BQ=26-3t,
∴AP=BQ,
∴26-3t=t,
t=
,
即经过
s时,四边形PQBA是矩形.
∵AP=t,CQ=3t,DP=24-t,
∴DP=CQ,
∴24-t=3t,
t=6,
即经过6s时,四边形PQCD是平行四边形;
(2)设经过ts时,四边形PQBA是矩形,
∵AP=t,CQ=3t,BQ=26-3t,
∴AP=BQ,
∴26-3t=t,
t=
| 13 |
| 2 |
即经过
| 13 |
| 2 |
点评:本题考查了梯形性质,平行四边形和矩形的性质的应用,注意:平行四边形的对边相等,矩形的对边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?