题目内容
已知二次函数 的图象经过点A(c,-2),
的图象经过点A(c,-2),
求证:这个二次函数图象的对称轴是x=3.(题目中的矩形框部分是一段被染了无法辨认的文字.)
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整.
解:(1)能.
由结论中的对称轴x=3,
得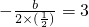 ,则b=-3,
,则b=-3,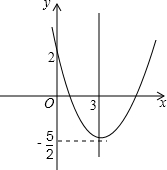
又因图象经过点A(c,2),
则: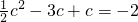 ,
,
c2-4c+4=0,(c-2)2=0,
∴c1=c2=2,
∴c=2.
∴二次函数解析式为y= x2-3x+2,
x2-3x+2,
图象如图所示:
(2)补:点B(0,2).(答案不唯一)
①过抛物线的任意一点的坐标,
②顶点坐标为(3,- ),
),
③当x轴的交点坐标(3+ ,0)或(3-
,0)或(3- ,0),
,0),
④当y轴的交点坐标为(0,2),
⑤b=-3或c=2.
分析:(1)根据对称轴坐标公式,可以求出b,然后把A(c,-2)代入可以求得c,从而得到二次函数解析式,进而在平面直角坐标系内画出函数的图象;
(2)已知题中有两个未知数,再添加一个条件能构成二元一次方程组即可.
点评:此题结合实际考查了二次函数解析式的求法,为一道条件开放性题目,需要掌握二次函数的性质才能解答.
由结论中的对称轴x=3,
得
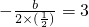 ,则b=-3,
,则b=-3,
又因图象经过点A(c,2),
则:
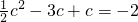 ,
,c2-4c+4=0,(c-2)2=0,
∴c1=c2=2,
∴c=2.
∴二次函数解析式为y=
 x2-3x+2,
x2-3x+2,图象如图所示:
(2)补:点B(0,2).(答案不唯一)
①过抛物线的任意一点的坐标,
②顶点坐标为(3,-
 ),
),③当x轴的交点坐标(3+
 ,0)或(3-
,0)或(3- ,0),
,0),④当y轴的交点坐标为(0,2),
⑤b=-3或c=2.
分析:(1)根据对称轴坐标公式,可以求出b,然后把A(c,-2)代入可以求得c,从而得到二次函数解析式,进而在平面直角坐标系内画出函数的图象;
(2)已知题中有两个未知数,再添加一个条件能构成二元一次方程组即可.
点评:此题结合实际考查了二次函数解析式的求法,为一道条件开放性题目,需要掌握二次函数的性质才能解答.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目