题目内容
在以点O为坐标原点的平面直角坐标系中,抛物线y=ax2+4ax+3a与轴交于A、B两点(OA>OB)与y轴负半轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)设直线x=m与抛物线交于点D,与线段AC交于点E,当线段DE的长取最大值时,求m的值和DE的长;
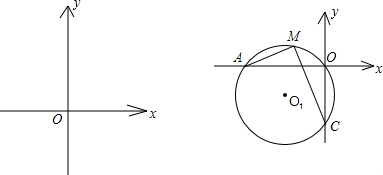
(3)设⊙01经过A、O、C三点,点M为弧AO上一点.求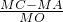 值.
值.

解:(1)由ax2+4ax+3a=0(a≠0),
可解得,x1=-1,x2=-3;
∵OA>OB,
∴A(-3,0),B(-1,0),
∴OC=3OB=3,
∵抛物线交y轴于负半轴,
∴C(0,-3),
∴3a=-3,a=-1,
∴抛物线解析式为y=-x2-4x-3;
(2)∵A(-3,0),C(0,-3),
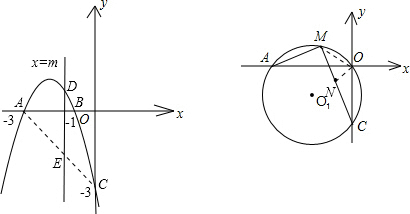 ∴直线AC的解析式为y=-x-3,
∴直线AC的解析式为y=-x-3,
易得,D(m,-m2-4m-3),E(m,-m-3),
∵抛物线开口向下,点E在AC之间,
∴-3<m<0,
∴DE=(-m2-4m-3)-(-m-3)
=-m2-3m=-(m+ )2+
)2+ ,
,
∴当m=- 时,DE的长取最大值,最大值为
时,DE的长取最大值,最大值为 ;
;
(3)在MC上截取N,使CN=AM,
易证,△CON≌△AOM(SAS),
∴ON=OM,△OMN为等腰直角三角形,故MN= MO,
MO,
∴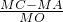 =
=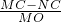 =
=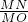 =
= .
.
分析:(1)令ax2+4ax+3a=0,求出与x轴、y轴的交点,再根据OC=3OB即可求出C点坐标,从而得到a的值,即可求出函数解析式;
(2)根据函数解析式求出D、E的坐标表达式,二者纵坐标之差为DE的长,其表达式为二次函数,从而通过配方可直接求出m的值和DE的长;
(3)在MC上截取N,使CN=AM,得到△CON≌△AOM,从而有ON=OM,则△OMN为等腰直角三角形,故MN= MO,再代入求值.
MO,再代入求值.
点评:本题考查了一元二次方程的解和二次函数与x轴的交点的横坐标的关系、二次函数求最值、相似三角形的性质和圆的性质,难度较大,要细心.
可解得,x1=-1,x2=-3;
∵OA>OB,
∴A(-3,0),B(-1,0),
∴OC=3OB=3,
∵抛物线交y轴于负半轴,
∴C(0,-3),
∴3a=-3,a=-1,
∴抛物线解析式为y=-x2-4x-3;
(2)∵A(-3,0),C(0,-3),
 ∴直线AC的解析式为y=-x-3,
∴直线AC的解析式为y=-x-3,易得,D(m,-m2-4m-3),E(m,-m-3),
∵抛物线开口向下,点E在AC之间,
∴-3<m<0,
∴DE=(-m2-4m-3)-(-m-3)
=-m2-3m=-(m+
 )2+
)2+ ,
,∴当m=-
 时,DE的长取最大值,最大值为
时,DE的长取最大值,最大值为 ;
;(3)在MC上截取N,使CN=AM,
易证,△CON≌△AOM(SAS),
∴ON=OM,△OMN为等腰直角三角形,故MN=
 MO,
MO,∴
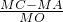 =
=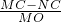 =
= =
= .
.分析:(1)令ax2+4ax+3a=0,求出与x轴、y轴的交点,再根据OC=3OB即可求出C点坐标,从而得到a的值,即可求出函数解析式;
(2)根据函数解析式求出D、E的坐标表达式,二者纵坐标之差为DE的长,其表达式为二次函数,从而通过配方可直接求出m的值和DE的长;
(3)在MC上截取N,使CN=AM,得到△CON≌△AOM,从而有ON=OM,则△OMN为等腰直角三角形,故MN=
 MO,再代入求值.
MO,再代入求值.点评:本题考查了一元二次方程的解和二次函数与x轴的交点的横坐标的关系、二次函数求最值、相似三角形的性质和圆的性质,难度较大,要细心.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 如图:在以点O为坐标原点的平面直角坐标系中,已知B(0,4),A(3,0),且DB=12,DA=13
如图:在以点O为坐标原点的平面直角坐标系中,已知B(0,4),A(3,0),且DB=12,DA=13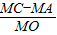 值.
值.