题目内容
已知一次函数y1=k1x+b1(k1≠0)的图象l1经过点B(-2,-2),一次函数y2=k2x+b2(k2≠0)的图象l2经过点C(2,-2),l1与l2相交于点A(0,2).
(1)求直线l1与l2的解析式,并在以点O为坐标原点的同一平面直角坐标系中画出它们的图象;
(2)连接BC,求△ABC的面积.
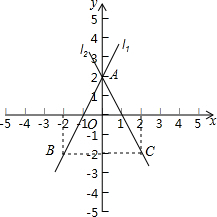 解:(1)∵一次函数y1=k1x+b1(k1≠0)的图象l1经过点B(-2,-2),A(0,2).
解:(1)∵一次函数y1=k1x+b1(k1≠0)的图象l1经过点B(-2,-2),A(0,2).∴
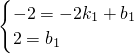 ,
,解得:
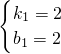 ,
,∴直线l1的解析式y1=2x+2,
∵一次函数y2=k2x+b2(k2≠0)的图象l2经过点C(2,-2),点A(0,2).
∴
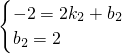 ,
,解得
 ,
,∴直线l2的解析式y1=-2x+2;
(2)△ABC的面积:
 ×4×4=8.
×4×4=8.分析:(1)利用待定系数法把B(-2,-2),A(0,2)代入一次函数y1=k1x+b1(k1≠0)中即可算出直线l1的解析式,把点C(2,-2),点A(0,2)代入一次函数y2=k2x+b2(k2≠0)可得直线l2的解析式;
(2)利用三角形的面积公式结合A、B、C三点坐标可得答案.
点评:此题主要考查了待定系数法求一次函数解析式,以及三角形的面积公式,关键是掌握凡是函数图象经过的点,必能满足解析式.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
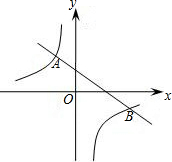 2,4)、(4,-2).
2,4)、(4,-2). (2012•德阳)已知一次函数y1=x+m的图象与反比例函数
(2012•德阳)已知一次函数y1=x+m的图象与反比例函数 已知一次函数y1=ax+b的图象与反比例函数y2=
已知一次函数y1=ax+b的图象与反比例函数y2= 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )