Question

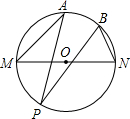如图，MN是⊙O的直径，∠PBN=50°，则∠MAP等于（　　）

A．50°

B．40°

C．30°

D．20°

Answer 1

分析：连接OP，可得∠MAP=

1

2

∠MOP，∠NBP=

1

2

∠NOP，已知MN为直径，可得∠MOP+∠NBP=180°，继而可得∠MAP+∠NBP=90°，最后可求解．

解答：解：连接OP，
可得∠MAP=

1

2

∠MOP，∠NBP=

1

2

∠NOP，
∵MN为直径，
∴∠MOP+∠NBP=180°，
∴∠MAP+∠NBP=90°，
∵∠PBN=50°，
∴∠MAP=90°-∠PBN=40°．
故选B．

点评：本题考查了圆周角定理的应用，能熟练地运用定理进行推理和计算是解答此题的关键，具有一定的代表性，难度适中．