题目内容
【题目】二轮自行车的后轮磨损比前轮要大，当轮胎的磨损度（%）达到100时，轮胎就报废了，当两个轮的中的一个报废后，自行车就不可以继续骑行了．过去的资料表明：把甲、乙两个同质、同型号的新轮胎分别安装在一个自行车的前、后轮上后，甲、乙轮胎的磨损度（%）y1、y2与自行车的骑行路程x （百万米）都成正比例关系，如图（1）所示：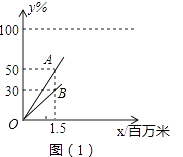 
（1）线段OB表示的是（填“甲”或“乙”），它的表达式是（不必写出自变量的取值范围）；
（2）求直线OA的表达式，根据过去的资料，这辆自行车最多可骑行多少百万米？
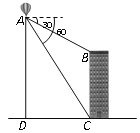
（3）爱动脑筋的小聪，想了一个增大自行车骑行路程的方案：如图（2），当自行车骑行a百万米后，我们可以交换自行车的前、后轮胎，使得甲、乙两个轮胎在b百万米处，同时报废，请你确定方案中a、b的值． 
【答案】
（1）甲；y=20x
（2）解：设直线OA的表达式为y=mx，
根据题意得：1.5m=50，
解得：m= 
，
则OA的解析式是y= x．
当y=100时，100= x，
解得：x=3．
答：这辆自行车最多可骑行3百万米
（3）解：根据题意，得
，
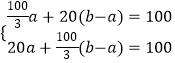解这个方程组，得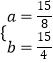 
【解析】解：（1）线段OB表示的是甲，设OB的解析式是y=kx，
则1.5k=30，
解得：k=20，
则OB的表达式是y=20x．
故答案是：甲，y=20x；
（1）根据图象可得OB表示的轮胎比OA表示的轮胎磨损慢，据此即可确定是甲或乙，利用待定系数法即可求得函数解析式；（2）利用待定系数法求得OA的函数解析式，然后求得当y=100时对应的x的值即可；（3）根据两个轮胎的磨损度都是100，即可列出方程组求解．
练习册系列答案
相关题目
