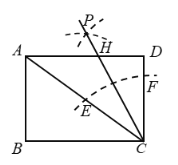
题目内容
【题目】已知：如图，在四边形ABCD中，AB⊥AC，DC⊥AC，∠B=∠D，
，
，
，点E，F分别是BC，AD的中点．
（1）求证：
；
（2）当
与
满足什么数量关系时，四边形
是正方形？请证明．
【答案】（1）见解析；（2）当
时，四边形
是正方形，理由见解析
【解析】
（1）先证明
得到
，
，由点E，F分别是BC，AD的中点得
，
，然后运用SSS证明
即可；
（2）易证四边形
是平行四边形，再证明四边形是平行四边形，证明AE=EC得平行四边形是菱形，由，点
是
的中点可证明菱形是正方形．
（1）证明：∵
，
，
∴
∵
，
∴
∴，
∵点
分别是，
的中点
∴
，
，
∴
∴
（2）当时，四边形是正方形
理由：
∵，
∴四边形是平行四边形，
∴
∵点分别是，的中点
∴
，
，
∴
∴四边形是平行四边形．
∵
，点是的中点
∴
∴平行四边形是菱形
∵，点是的中点
∴
即
∴菱形是正方形．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
【题目】某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数．
类别 | 频数（人数） | 频率 |
武术类 | 0.20 | |
书画类 | 15 | 0.l5 |
棋牌类 | 25 |
|
器乐类 | ||
合计 |
| 1.00 |
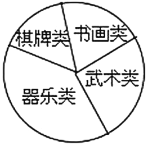
（1）确定调查方式时，甲同学说：“我到七年级（1）班去调查全体同学”；乙同学说：“放学时我到校门口随机调查部分同学”；丙同学说：“我到七年级每个班随机调查一定数量的同学”．请指出哪位同学的调查方式最合理．
（2）他们采用了最为合理的调查方法收集数据，并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题：
①
____，
_____；
②在扇形统计图中，器乐类所对应扇形的圆心角是_____度；
③若该校七年级有学生460人，请你估计大约有多少学生参加武术类校本课程．
