题目内容
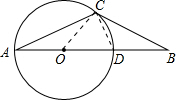
 (2013•乐清市模拟)如图,在△ABC中,点O在AB边上,以O为圆心的圆经过A,C两点,交AB于点D,且2∠A+∠B=90°,
(2013•乐清市模拟)如图,在△ABC中,点O在AB边上,以O为圆心的圆经过A,C两点,交AB于点D,且2∠A+∠B=90°,(1)求证:BC是⊙O的切线.
(2)若OA=6,且OD=BD,求AC的长.
分析:(1)连接OC,由同弧所对的圆心角等于所对圆周角的2倍得到∠COD=2∠A,由2∠A与∠B之和为90度,得到∠COD与∠B互余,在三角形COB中,得到∠OCB为直角,即可确定出BC为圆O的切线;
(2)连接CD,可证明直角三角形ACD中∠A=30°,利用锐角三角函数即可求出AC的长.
(2)连接CD,可证明直角三角形ACD中∠A=30°,利用锐角三角函数即可求出AC的长.
解答:(1)证明:连接OC,
∵
=
,
∴∠COD=2∠A,
∵2∠A+∠B=90°,
∴∠COD+∠B=90°,
在△OCB中,∠OCB=90°,
∴BC是⊙O的切线;
(2)连接CD,
∵∠COB=2∠A,2∠A+∠B=90°,
∴∠B+∠COA=90°,
∵CD=
BO,
∵OD=BD,
∴CD=
AD,
∴∠A=30°
∴cos30°=
,
∵AD=2AB=12,
∴AC=6
.
∵
 |
| CD |
 |
| CD |

∴∠COD=2∠A,
∵2∠A+∠B=90°,
∴∠COD+∠B=90°,
在△OCB中,∠OCB=90°,
∴BC是⊙O的切线;
(2)连接CD,
∵∠COB=2∠A,2∠A+∠B=90°,
∴∠B+∠COA=90°,
∵CD=
| 1 |
| 2 |
∵OD=BD,
∴CD=
| 1 |
| 2 |
∴∠A=30°
∴cos30°=
| AC |
| AD |
∵AD=2AB=12,
∴AC=6
| 3 |
点评:此题考查了切线的判定,特殊角的锐角三角函数以及圆周角定理,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 (2013•乐清市模拟)某校开展大课间活动,某班同学积极响应,某班同学参加大课间活动项目情况的扇形统计图该班同学参加体育项目情况的扇形统计图如图所示,由图可知参加人数最多的活动是( )
(2013•乐清市模拟)某校开展大课间活动,某班同学积极响应,某班同学参加大课间活动项目情况的扇形统计图该班同学参加体育项目情况的扇形统计图如图所示,由图可知参加人数最多的活动是( ) (2013•乐清市模拟)如图,点D在△ABC的边BC上,过点D作DF∥AB,交AC于点E,连结BF,已知BD:DC=1:2,DE:EF=1:3,则S△ABC:S△BDF=( )
(2013•乐清市模拟)如图,点D在△ABC的边BC上,过点D作DF∥AB,交AC于点E,连结BF,已知BD:DC=1:2,DE:EF=1:3,则S△ABC:S△BDF=( ) (2013•乐清市模拟)如图,在四边形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直线上的一个动点,当
(2013•乐清市模拟)如图,在四边形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直线上的一个动点,当