题目内容
 (2013•乐清市模拟)如图,在四边形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直线上的一个动点,当
(2013•乐清市模拟)如图,在四边形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直线上的一个动点,当AE=
9或
或
或
| 4 |
| 5 |
5+
| ||
| 2 |
5-
| ||
| 2 |
9或
或
或
时,△CDE是直角三角形.| 4 |
| 5 |
5+
| ||
| 2 |
5-
| ||
| 2 |
分析:建立坐标系,则A的坐标是(0,5),C的坐标是(5,0),D的坐标是(1,5).分C、D、E分别是直角顶点三种情况进行讨论,当C是直角顶点时,求得CE的解析式,求得E的坐标即可求得AE的长,同理求得当D是直角顶点时AE的长,当E是直角顶点时,根据直角三角形斜边上的中线等于斜边的一半即可求得E的坐标,进而求得AE的长.
解答: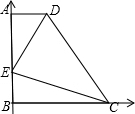 解:如图建立坐标系,则A的坐标是(0,5),C的坐标是(5,0),D的坐标是(1,5).
解:如图建立坐标系,则A的坐标是(0,5),C的坐标是(5,0),D的坐标是(1,5).
设直线CD的解析式是y=kx+b,则
,
解得:
,
则CD的解析式是:y=-
x+
,
在直角△CDE中,当C是直角顶点时,设CE的坐标是:y=
x+a,把C的坐标代入得:4+a=0,解得:a=-4,则CE的解析式是y=
x-4,令x=0,解得:y=-4,则E的坐标是(0,-4),则AE=9;
同理,当D是直角顶点时,设DE的坐标是:y=
x+b,把D的坐标代入得:
+b=5,解得:a=
,则DE的解析式是y=
x+
,令x=0,解得:y=
,则E的坐标是(0,
),则AE=
;
当E是直角顶点时,CD=
=
,CD的中点是(3,
),设E的坐标是(0,c),
则
=
×
,
解得:c=
,
故E的坐标是(0,
)或(0,
),
则AE=
或
.
故答案是:9或
或
或
.
 解:如图建立坐标系,则A的坐标是(0,5),C的坐标是(5,0),D的坐标是(1,5).
解:如图建立坐标系,则A的坐标是(0,5),C的坐标是(5,0),D的坐标是(1,5).设直线CD的解析式是y=kx+b,则
|
解得:
|
则CD的解析式是:y=-
| 5 |
| 4 |
| 25 |
| 4 |
在直角△CDE中,当C是直角顶点时,设CE的坐标是:y=
| 4 |
| 5 |
| 4 |
| 5 |
同理,当D是直角顶点时,设DE的坐标是:y=
| 4 |
| 5 |
| 4 |
| 5 |
| 21 |
| 5 |
| 4 |
| 5 |
| 21 |
| 5 |
| 21 |
| 5 |
| 21 |
| 5 |
| 4 |
| 5 |
当E是直角顶点时,CD=
| 52+(5-1)2 |
| 41 |
| 5 |
| 2 |
则
32+(c-
|
| 1 |
| 2 |
| 41 |
解得:c=
5±
| ||
| 2 |
故E的坐标是(0,
5+
| ||
| 2 |
5-
| ||
| 2 |
则AE=
5+
| ||
| 2 |
5-
| ||
| 2 |
故答案是:9或
| 4 |
| 5 |
5+
| ||
| 2 |
5-
| ||
| 2 |
点评:本题考查了待定系数法求函数的解析式,以及直角三角形的性质,正确求得当E是直角三角形的直角顶点时E的坐标是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (2013•乐清市模拟)某校开展大课间活动,某班同学积极响应,某班同学参加大课间活动项目情况的扇形统计图该班同学参加体育项目情况的扇形统计图如图所示,由图可知参加人数最多的活动是( )
(2013•乐清市模拟)某校开展大课间活动,某班同学积极响应,某班同学参加大课间活动项目情况的扇形统计图该班同学参加体育项目情况的扇形统计图如图所示,由图可知参加人数最多的活动是( ) (2013•乐清市模拟)如图,点D在△ABC的边BC上,过点D作DF∥AB,交AC于点E,连结BF,已知BD:DC=1:2,DE:EF=1:3,则S△ABC:S△BDF=( )
(2013•乐清市模拟)如图,点D在△ABC的边BC上,过点D作DF∥AB,交AC于点E,连结BF,已知BD:DC=1:2,DE:EF=1:3,则S△ABC:S△BDF=( ) (2013•乐清市模拟)如图,在△ABC中,点O在AB边上,以O为圆心的圆经过A,C两点,交AB于点D,且2∠A+∠B=90°,
(2013•乐清市模拟)如图,在△ABC中,点O在AB边上,以O为圆心的圆经过A,C两点,交AB于点D,且2∠A+∠B=90°,