题目内容
【题目】已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
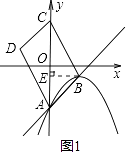
(1)如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式.
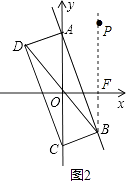
(2)如图2,若抛物线y=a(x﹣m)2+n(m>0)的伴随直线是y=x﹣3,伴随四边形的面积为12,求此抛物线的解析式.
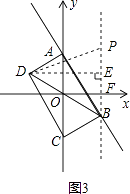
(3)如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.
①用含b的代数式表示m、n的值;
②在抛物线的对称轴上是否存在点P,使得△PBD是一个等腰三角形?若存在,请直接写出点P的坐标(用含b的代数式表示);若不存在,请说明理由.
【答案】
(1)
解:由抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,
∴抛物线y=(x﹣2)2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),
设所求直线解析式为y=kx+b,
∴ ![]() ,
,
解得: ![]() ,
,
∴所求直线解析式为y=﹣2x+5
(2)
解:如图,作BE⊥AC于点E,由题意得四边形ABCD是平行四边形,
点A的坐标为(0,﹣3),
点C的坐标为(0,3),
可得:AC=6,
∵平行四边形ABCD的面积为12,
∴S△ABC=6即S△ABC= ![]() ACBE=6,
ACBE=6,
∴BE=2,
∵m>0,即顶点B在y轴的右侧,且在直线y=x﹣3上,
∴顶点B的坐标为(2,﹣1),
又抛物线经过点A(0,﹣3),
∴a=﹣ ![]() ,
,
∴y=﹣ ![]() (x﹣2)2﹣1
(x﹣2)2﹣1
(3)
解:①如图,作BF⊥x轴于点F,
由已知可得A坐标为(0,b),C点坐标为(0,﹣b),
∵顶点B(m,n)在直线y=﹣2x+b(b>0)上,
∴n=﹣2m+b,即点B点的坐标为(m,﹣2m+b),
在矩形ABCD中,CO=BO.
∴b= ![]() ,
,
∴b2=m2+4m2﹣4mb+b2,
∴m= ![]() b,
b,
n=﹣2× ![]() b+b=﹣
b+b=﹣ ![]() b,
b,
②∵B点坐标为(m,n),即( ![]() b,﹣
b,﹣ ![]() b),
b),
∴BO= ![]() =b,
=b,
∴BD=2b,
当BD=BP,
∴PF=2b﹣ ![]() b=
b= ![]() b,
b,
∴P点的坐标为( ![]() b,
b, ![]() b);
b);
如图3,当DP=PB时,
过点D作DE⊥PB,于点E,
∵B点坐标为( ![]() b,﹣
b,﹣ ![]() b),
b),
∴D点坐标为(﹣ ![]() b,
b, ![]() b),
b),
∴DE= ![]() b,BE=
b,BE= ![]() b,设PE=x,
b,设PE=x,
∴DP=PB= ![]() b+x,
b+x,
∴DE2+PE2=DP2,
∴ ![]() +x2=(
+x2=( ![]() b+x)2,
b+x)2,
解得:x= ![]() b,
b,
∴PF=PE+EF= ![]() b+
b+ ![]() b=
b= ![]() b,
b,
∴此时P点坐标为:( ![]() b,
b, ![]() b);
b);
同理P可以为( ![]() b,﹣
b,﹣ ![]() b);(
b);( ![]() b,
b, ![]() b),
b),
故P点坐标为:( ![]() b,
b, ![]() b);(
b);( ![]() b,
b, ![]() b);(
b);( ![]() b,﹣
b,﹣ ![]() b);(
b);( ![]() b,
b, ![]() b).
b).
【解析】(1)利用抛物线y=(x﹣2)2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),求出直线解析式即可;(2)首先得出点A的坐标为(0,﹣3),以及点C的坐标为(0,3),进而求出BE=2,得出顶点B的坐标求出解析式即可;(3)①由已知可得A坐标为(0,b),C点坐标为(0,﹣b),以及n=﹣2m+b,即点B点的坐标为(m,﹣2m+b),利用勾股定理求出;②利用①中B点坐标,以及BD的长度即可得出P点的坐标.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 名校课堂系列答案
名校课堂系列答案