题目内容
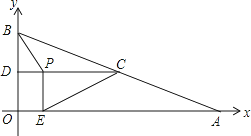
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
A.![]()
B.![]()
C.![]()
D.2![]()
【答案】B
【解析】作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案:
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小.
∵DP=PA,∴PA+PC=PD+PC=CD.
∵B(3,![]() ),∴AB=
),∴AB=![]() ,OA=3,∠B=60°.
,OA=3,∠B=60°.
由勾股定理得:OB=2![]() .
.
由三角形面积公式得:![]() ×OA×AB=
×OA×AB=![]() ×OB×AM,∴AM=
×OB×AM,∴AM=![]() .∴AD=2×
.∴AD=2×![]() =3.
=3.
∵∠AMB=90°,∠B=60°,∴∠BAM=30°.
∵∠BAO=90°,∴∠OAM=60°.
∵DN⊥OA,∴∠NDA=30°.∴AN=![]() AD=
AD=![]() .
.
由勾股定理得:DN=![]() .
.
∵C(![]() ,0),∴
,0),∴![]() .
.
在Rt△DNC中,由勾股定理得:![]() .
.
∴PA+PC的最小值是![]() .
.
故选B.
【考点精析】认真审题,首先需要了解含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下2×2列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
(Ⅰ)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
(Ⅱ)根据以上2×2列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)