题目内容
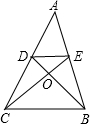如图，△OED∽△OCB，且OE=6，EC=21，则△OCB与△OED的相似比是
- A.
- B.
- C.
- D.
B
分析：三角形的相似比即为相似三角形对应边长的比，所以题中求△OCB与△OED的相似比，由线段OE与EC的长，即可求解OC与OE的比值即可．
解答：∵△OED∽△OCB，三角形的相似比等于相似三角形对应边的比，
∴△OCB与△OED的相似比即为OC与OE的比值，
又OE=6，EC=21，
∴OC：OE=（21-6）：6=15：6=5：2，
故选B．
点评：本题主要考查了相似三角形的性质问题，理解三角形的相似比即为其对应边的比值．
分析：三角形的相似比即为相似三角形对应边长的比，所以题中求△OCB与△OED的相似比，由线段OE与EC的长，即可求解OC与OE的比值即可．
解答：∵△OED∽△OCB，三角形的相似比等于相似三角形对应边的比，
∴△OCB与△OED的相似比即为OC与OE的比值，
又OE=6，EC=21，
∴OC：OE=（21-6）：6=15：6=5：2，
故选B．
点评：本题主要考查了相似三角形的性质问题，理解三角形的相似比即为其对应边的比值．
练习册系列答案
备战中考寒假系列答案
相关题目
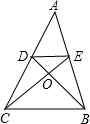如图，△OED∽△OCB，且OE=6，EC=21，则△OCB与△OED的相似比是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
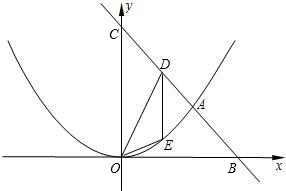
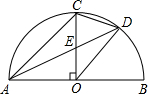（2011•武汉模拟）如图，AB是半圆直径，半径OC⊥AB于点D，AD平分∠CAB交弧
