题目内容
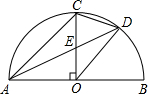 (2011•武汉模拟)如图,AB是半圆直径,半径OC⊥AB于点D,AD平分∠CAB交弧
(2011•武汉模拟)如图,AB是半圆直径,半径OC⊥AB于点D,AD平分∠CAB交弧 |
| BC |
分析:根据等腰三角形的性质和角平分线的性质,利用等量代换求证∠CAD=∠ADO即可;过点E作EF⊥AC,根据角平分线上的点到角的两边的距离相等可得OE=EF,再根据直角三角形斜边大于直角边可证;再根据内角与外角的关系进行判断即可得出答案.
解答: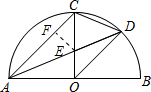 解:①∵AB是半圆直径,
解:①∵AB是半圆直径,
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=
∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∴①正确.
②过点E作EF⊥AC,
∵OC⊥AB,AD平分∠CAB交弧BC于点D,
∴OE=EF,
在Rt△EFC中,CE>EF,
∴CE>OE,
∴②错误.
③∵在△ODE和△ADO中,
∠DEO=90°+∠DAO,
∠AOD=90°+∠COD,
∵∠DAO=
∠COD,
∴③∠OED=∠AOD错误;
④作ON⊥CD,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=
×45°=22.5°,
∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°,
∠AEO=90°-22.5°=67.5°,
∴∠DCE=∠CED=67.5°,
∴CD=DE,
∴④正确.
综上所述,只有①④正确.
故选:B.
 解:①∵AB是半圆直径,
解:①∵AB是半圆直径,∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=
| 1 |
| 2 |
∴∠CAD=∠ADO,
∴AC∥OD,
∴①正确.
②过点E作EF⊥AC,
∵OC⊥AB,AD平分∠CAB交弧BC于点D,
∴OE=EF,
在Rt△EFC中,CE>EF,
∴CE>OE,
∴②错误.
③∵在△ODE和△ADO中,
∠DEO=90°+∠DAO,
∠AOD=90°+∠COD,
∵∠DAO=
| 1 |
| 2 |
∴③∠OED=∠AOD错误;
④作ON⊥CD,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=
| 1 |
| 2 |

∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°,
∠AEO=90°-22.5°=67.5°,
∴∠DCE=∠CED=67.5°,
∴CD=DE,
∴④正确.
综上所述,只有①④正确.
故选:B.
点评:此题主要考查相似三角形的判定与性质,圆心角、弧、弦的关系,圆周角定理,等腰三角形的性质,三角形内角和定理等知识点的灵活运用,此题步骤繁琐,但相对而言,难易程度适中,很适合学生的训练是一道典型的题目.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
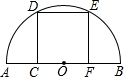 (2011•武汉模拟)如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则,以AC和BC的长为两根的一元二次方程是( )
(2011•武汉模拟)如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则,以AC和BC的长为两根的一元二次方程是( )