题目内容
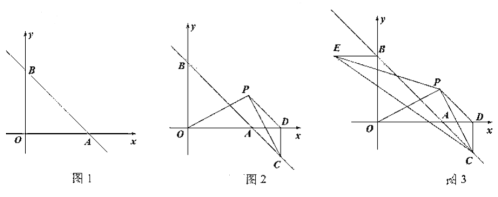
【题目】如图,已知关于![]() 的一元二次函数
的一元二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.
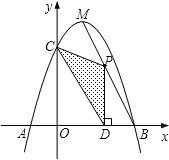
⑴ 求出一元二次函数的关系式;
⑵ 点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
⑶ 探索线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为直角三角形,如果存在,求出
为直角三角形,如果存在,求出![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() );(3)P点坐标为:
);(3)P点坐标为:![]() ,
,![]() .
.
【解析】
(1)可根据OB、OC的长得出B、C两点的坐标,然后用待定系数法即可求出抛物线的解析式.
(2)求出P点的坐标,据此可根据三角形的面积计算方法求出S与m的函数关系式.
(3)先根据抛物线的解析式求出M的坐标,进而可得出直线BM的解析式,以及P点纵坐标,即可得出符合条件的P点的坐标.
解:⑴![]() 、
、![]() .
.
![]()
解得![]() ,
,
所以![]()
⑵∵y=-x2+2x+3=-(x-1)2+4,
∴![]() .
.
设![]() :
:![]() ,
,
则![]() 得
得![]() 所以
所以![]() .
.
所以![]() ,
,
![]() (
(![]() )
)
(3)∵若∠PDC是直角,则点C在x轴上,由函数图象可知点C在y轴的正半轴上,
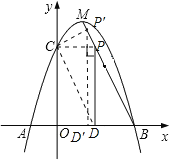
∴∠PDC≠90°,
在△PCD中,当∠DPC=90°时,
当CP∥AB时,
∵PD⊥AB,
∴CP⊥PD,
∴PD=OC=3,
∴P点纵坐标为:3,代入y=-2x+6,
![]() ,此时P
,此时P![]() ,
,
当∠P′CD′=90°时,△COD′∽△D′CP′,
此时CD′2=COP′D′,
即9+m2=3(-2m+6),
∴m2+6m-9=0,
解得:![]() ,
,
∵1≤m<3,
![]() ,
,
![]() ,
,
综上所述:P点坐标为:![]() ,
,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目