题目内容
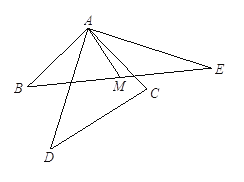
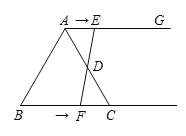
【题目】如图,在等边三角形ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动;同时点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s).
(1)△ABC的BC边上的高为_________cm;
(2)连接EF,当EF经过AC的中点D时,求证:△ADE≌△CDF;
(3)求当t为何值时,AC与EF互相平分;
(4)当t=________s时,四边形ACFE是菱形.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)6
;(4)6
【解析】
(1)根据等边三角形三线合一即可求解;
(2)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;
(3)根据AC与EF互相平分,可得△ADE≌△CDF,可得AE=CF即![]() ,故可求解;
,故可求解;
(4)若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可.
解:(1)如图,过A点作AH⊥BC于H点
∵△ABC是等边三角形,BC=6 cm
∴BH=![]() BC=3cm
BC=3cm
∴AH=![]() =
=![]() cm
cm
故答案为:![]() .
.

(2)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
 ,
,
∴△ADE≌△CDF(AAS);
(3)若AC与EF互相平分,
则AD=CD,ED=FD,又∠ADE=∠CDF
∴△ADE≌△CDF.
∴AE=CF.
∴![]() .
.
解得![]() .
.
(4)若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).
故答案为:6.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目