题目内容
如图所示,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕O点顺时针旋转30°后,恰好A点在双曲线y= (x>0)上.
(x>0)上.(1)求双曲线y=
 (x>0)的解析式;
(x>0)的解析式;(2)等边三角形OAB继续按顺时针方向旋转多少度后,A点再次落在双曲线上?
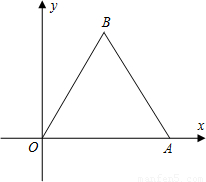
【答案】分析:(1)在Rt△AOD中,OA=2,∠AOD=30°,就可以求出OD,AD的长度,就得到A点的坐标,代入双曲线y= (x>0)就可以求出函数的解析式;
(x>0)就可以求出函数的解析式;
(2)作出函数的图象,根据图象就可以得到.然后进行验证即可.
解答: 解:(1)如图所示,
解:(1)如图所示,
OA=2,∠AOD=30°,
在Rt△AOD中,
∴OD=OA•cos30°=2× =
=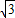 ,
,
AD=OA•sin30°=2× =1.
=1.
∴A( ,-1),
,-1),
把x= ,y=-1代入y=
,y=-1代入y= ,
,
∴k=- .
.
∴双曲线的解析式为y=- (x>0);
(x>0);

(2)猜想等边三角形OAB继续按顺时针方向旋转30°后,A点再次落在双曲线上,
如图,此时A(1,- ),代入y=-
),代入y=- 满足,
满足,
故猜想正确.
点评:本题通过反比例函数的知识,考查学生的猜想探究能力.解题时先直观地猜想,再按照从特殊到一般的方法去验证.
 (x>0)就可以求出函数的解析式;
(x>0)就可以求出函数的解析式;(2)作出函数的图象,根据图象就可以得到.然后进行验证即可.
解答:
 解:(1)如图所示,
解:(1)如图所示,OA=2,∠AOD=30°,
在Rt△AOD中,
∴OD=OA•cos30°=2×
 =
=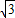 ,
,AD=OA•sin30°=2×
 =1.
=1.∴A(
 ,-1),
,-1),把x=
 ,y=-1代入y=
,y=-1代入y= ,
,∴k=-
 .
.∴双曲线的解析式为y=-
 (x>0);
(x>0);
(2)猜想等边三角形OAB继续按顺时针方向旋转30°后,A点再次落在双曲线上,
如图,此时A(1,-
 ),代入y=-
),代入y=- 满足,
满足,故猜想正确.
点评:本题通过反比例函数的知识,考查学生的猜想探究能力.解题时先直观地猜想,再按照从特殊到一般的方法去验证.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则tan∠AED的值等于( )
如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则tan∠AED的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于
如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于 将△OAB绕点O顺时针旋转30°后,得到△OB′A′,点A′恰好落在双曲线y=
将△OAB绕点O顺时针旋转30°后,得到△OB′A′,点A′恰好落在双曲线y= 23、高为50cm,底面周长为50cm的圆柱,在此圆柱的侧面上划分(如图所示)边长为lcm的正方形,用四个边长为lcm的小正方形构成“T”字形,用此图形是否能拼成圆柱侧面?试说明理由.
23、高为50cm,底面周长为50cm的圆柱,在此圆柱的侧面上划分(如图所示)边长为lcm的正方形,用四个边长为lcm的小正方形构成“T”字形,用此图形是否能拼成圆柱侧面?试说明理由. 如图所示,边长为1 的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕点O逆时针旋转90°.
如图所示,边长为1 的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕点O逆时针旋转90°.