题目内容
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理﹣﹣“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2 . 小明尝试对它进行证明,部分过程如下:
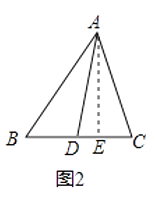
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2 ,
同理可得:AC2=AE2+CE2 , AD2=AE2+DE2 ,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=…
(1)请你完成小明剩余的证明过程;
理解运用: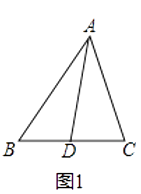
(2)①在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=;
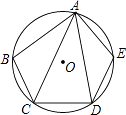
②如图3,⊙O的半径为6,点A在圆内,且OA=2 ![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
拓展延伸: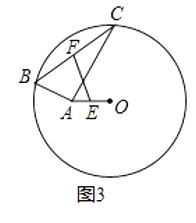
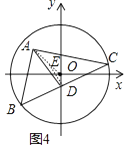
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5 ![]() ,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
请你利用上面的方法和结论,求出AD长的最大值.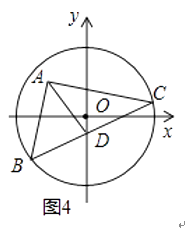
【答案】
(1)解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,为证明的方便,不妨设BD=CD=x,DE=y,
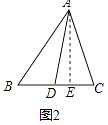
∴AB2+AC2=2AE2+(x+y)2+(x﹣y)=2AE2+2x2+2y2、
=2AE2+2BD2+2DE2=2AD2+2BD2
(2)![]() ,4
,4
(3)如图4中,连接OA,取OA的中点E,连接DE.
由(2)的②可知:DE═ ![]() OB2﹣
OB2﹣ ![]() OA2=
OA2= ![]() ,
,
在△ADE中,AE= ![]() ,DE=
,DE= ![]() ,
,
∵AD≤AE+DE,
∴AD长的最大值为 ![]() +
+ ![]() =10
=10
【解析】解:(2)①∵AB2+AC2=2AD2+2BD2,
∴62+42=2AD2+2×42,
∴AD= ![]()
②如图3中,
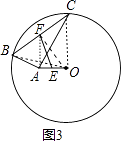
∵AF是△ABC的中线,EF是△AEO的中线,OF是△BOC的中线,
∵2EF2+2AE2=AF2+OF2,
2AF2+2BF2=AB2+AC2,
OF2=OB2﹣BF2,
∴4EF2=2OB2﹣4AE2=2OB2﹣OA2,
∴EF=2= ![]() OB2﹣
OB2﹣ ![]() OA2=16,
OA2=16,
∴EF=4(负根以及舍弃),
所以答案是 ![]() .4.
.4.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】某城市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计费;月用水量超过20m3时,超过部分按2.6元/m3计费.设每户家庭的月用水量为xm3时,应交水费y元.
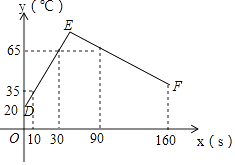
(1)试求出0≤x≤20和x>20时,y与x之间的函数关系;
(2)小明家第二季度用水量的情况如下:
月份 | 四月 | 五月 | 六月 |
用水量(m3) | 15 | 17 | 21 |
小明家这个季度共缴纳水费多少元?
【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
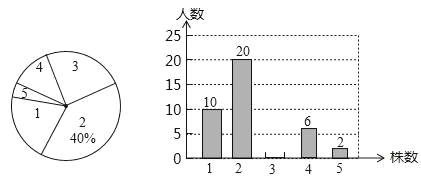
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).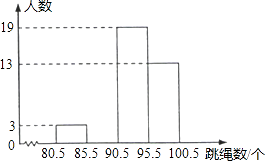
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.