题目内容
已知a、b、c是互不相等的实数,且
=
=
,则x+y+z的值为( )
| x |
| a-b |
| y |
| b-c |
| z |
| c-a |
| A、-1 | B、0 | C、1 | D、2 |
分析:设
=
=
=k,则x=k(a-b),y=k(b-c),z=k(c-a),三式相加即可得出答案.
| x |
| a-b |
| y |
| b-c |
| z |
| c-a |
解答:解:设
=
=
=k,
则x=k(a-b),y=k(b-c),z=k(c-a),
∴x+y+z=k(a-b)+k(b-c)+k(c-a)=0.
故选B.
| x |
| a-b |
| y |
| b-c |
| z |
| c-a |
则x=k(a-b),y=k(b-c),z=k(c-a),
∴x+y+z=k(a-b)+k(b-c)+k(c-a)=0.
故选B.
点评:本题考查了分式的化简求值,难度适中,关键是正确设出
=
=
=k.
| x |
| a-b |
| y |
| b-c |
| z |
| c-a |

练习册系列答案
相关题目
已知a,b,c是互不相等的正实数,且
=
=
,则代数式
的值为( )
| a-b |
| x |
| b-c |
| y |
| c-a |
| z |
| 2011x+2011y+2011z |
| 2009a+2010b+2011c |
| A、2009 | B、2010 |
| C、2011 | D、0 |
已知a,b,c是互不相等的正实数,且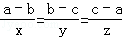 ,则代数式
,则代数式 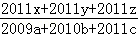 的值为( )
的值为( )
| A.2009 | B.2010 | C.2011 | D.0 |
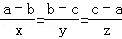 ,则代数式
,则代数式 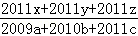 的值为( )
的值为( )