��Ŀ����
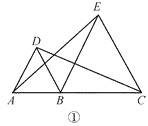
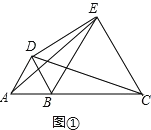
����Ŀ����ֱ����˳��ȡ A��B��C ���㣬�ֱ��� AB��BC Ϊ�߳���ֱ�ߵ�ͬ�����������Σ� ���������������ε���һ����ֱ�Ϊ D��E��
(1)��ͼ�٣����� CD��AE����֤��CD��AE��
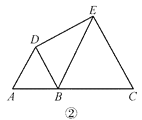
(2)��ͼ�ڣ��� AB��1��BC��2���� DE �ij���
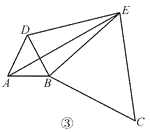
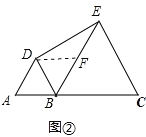
(3)��ͼ�ۣ���ͼ���е��������� BCE �� B �����ʵ�����ת������ AE������ DE2��BE2�� AE2�������DEB �Ķ�����
���𰸡�������
�������������������1������ABD����ECB���ǵȱ������οɵ�AD=AB=BD��BC=BE=EC����ABD=��EBC=60�������ԡ�ABE=��DBC��������ABE�ա�DBC������֤��AE=DC����2��
��ͼ���У�ȡBE�е�F������DF�������ⲻ�ѵó�BF=EF=1=BD���ٽ�ϡ�DBF=60���ɵ���DBF�ǵȱ������Σ������Ƴ���EDB=90�������ɹ��ɶ��������DE�ij�����3����ͼ���У�����DC������֪��������֤����ABE�ա�DBC������AE=DC����ΪDE2+BE2=AE2��BE=CE������DE2+CE2=CD2�����ԡ�DEC=90������Ϊ��BEC=60�������ԡ�DEB=��DEC����BEC=30����
���������
��1��֤������ͼ���У�
�ߡ�ABD����ECB���ǵȱ������Σ�
��AD=AB=BD��BC=BE=EC����ABD=��EBC=60����
���ABE=��DBC��
����ABE����DBC��
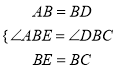 ��
��
���ABE�ա�DBC��
��AE=DC��
��2����ͼ���У�ȡBE�е�F������DF��
��BD=AB=1��BE=BC=2����ABD=��EBC=60����
��BF=EF=1=BD����DBF=60����
���DBF�ǵȱ���������
��DF=BF=EF����DFB=60����
�ߡ�BFD=��FED+��FDE��
���FDE=��FED=30����
���EDB=180������DBE����DEB=90����
��DE=![]() ��
��
��3����ͼ���У�����DC��
�ߡ�ABD�͡�ECB���ǵȱ������Σ�
��AD=AB=BD��BC=BE=EC����ABD=��EBC=60����
���ABE=��DBC��
�ڡ�ABE�͡�DBC�У�
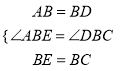 ��
��

����Ŀ��ijУ���꼶��1��������ίԱͳ����ȫ��ͬѧ60���������������г�������IJ�����Ƶ���ֲ����Ͳ�������Ƶ���ֲ�ֱ��ͼ������ͼ���е���Ϣ�������
��� | �������� | Ƶ�� |
A | 60��x��80 | 2 |
B | 80��x��100 | 6 |
C | 100��x��120 | 18 |
D | 120��x��140 | 12 |
E | 140��x��160 | a |
F | 160��x��180 | 3 |
G | 180��x��200 | 1 |
�ϼ� | 50 | |
��1����a��ֵ��
��2������������x��120��x��180��Χ�ڵ�ѧ����������
��3����ȫƵ���ֲ�ֱ��ͼ����ָ������������ֱ��Ƕ��٣�

����Ŀ��ijУ���꼶��1��������ίԱͳ����ȫ��ͬѧ60���������������г�������IJ�����Ƶ���ֲ����Ͳ�������Ƶ���ֲ�ֱ��ͼ������ͼ���е���Ϣ�������
��� | �������� | Ƶ�� |
A | 60��x��80 | 2 |
B | 80��x��100 | 6 |
C | 100��x��120 | 18 |
D | 120��x��140 | 12 |
E | 140��x��160 | a |
F | 160��x��180 | 3 |
G | 180��x��200 | 1 |
�ϼ� | 50 | |
��1����a��ֵ��
��2������������x��120��x��180��Χ�ڵ�ѧ����������
��3����ȫƵ���ֲ�ֱ��ͼ����ָ������������ֱ��Ƕ��٣�