题目内容
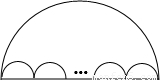
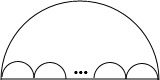如图，大半圆中有n个小半圆，大半圆弧长为L1，n个小半圆的弧长和为L2，找出L1和L2的关系并证明你的结论．（友情提示：利用弧长公式）
解：L1=L2．理由如下：
设n个小半圆半径依次为r1，r2，…，rn．
则大圆半径为（r1+r2+…+rn）
∴L1=π（r1+r2+…+rn），
L2=πr1+πr2+…+πrn
=π（r1+r2+…+rn），
∴L1=L2．
分析：根据周长公式分别写出L1和L2的表达式进行比较即可．
点评：本题考查了圆的认识，利用周长公式计算即可．
设n个小半圆半径依次为r1，r2，…，rn．
则大圆半径为（r1+r2+…+rn）
∴L1=π（r1+r2+…+rn），
L2=πr1+πr2+…+πrn
=π（r1+r2+…+rn），
∴L1=L2．
分析：根据周长公式分别写出L1和L2的表达式进行比较即可．
点评：本题考查了圆的认识，利用周长公式计算即可．
练习册系列答案
相关题目
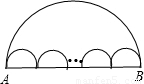
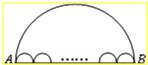10、如图，大半圆中有n个小半圆，现有甲、乙两虫停留在A处，如果甲虫沿着大半圆弧爬向B处，乙虫沿着n个小半圆弧爬向B处，并且假定甲、乙两虫的爬行速度相同，那么下列说法正确的是（ ）
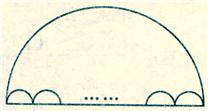4、如图，大半圆中有n个小半圆，大半圆弧长为L1，n个小半圆的弧长和为L2，找出L1和L2的关系并证明你的结论．（友情提示：利用弧长公式）
