题目内容
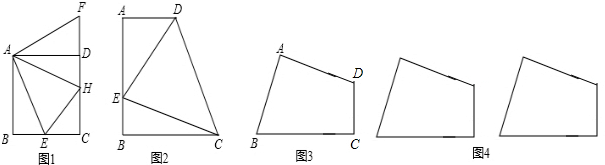
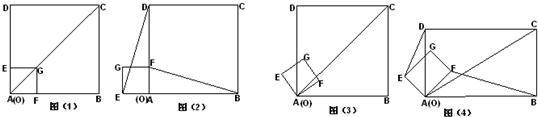
如图1,在正方形ABCD中,E是AD中点,F是BA延长线上一点,AB=2AF.
(1)试说明△ABE与△ADF能够完全重合.
(2)阅读下面材料.
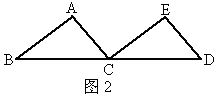
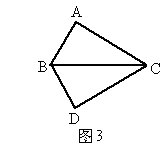

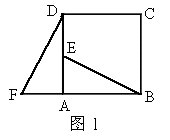
如图2,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;如图3,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图4,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.像这样,其中一个三角形是由另一个三角形按平移、翻折、旋转等方法变成的.这种只改变位置,不改变形状、大小的图形变换,叫做三角形的全等变换,回答下列问题:
①在图1中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
②指出图1中线段BE和DF之间的关系.
答案:
解析:
解析:
|
解: (1)AD=AB,∠DAB=90°,则点D绕A顺时针旋转90°可得到B点;AF=AE,∠FAE=90°,同理可知F绕A旋转90°到E点,因此△AFD绕点A顺时针旋转90°可得到△AEB,所以△ABE与△ADF能够完全重合.(2) ①通过旋转可使△ABE变到△ADF的位置.② BE=DF且BE⊥DF. |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明.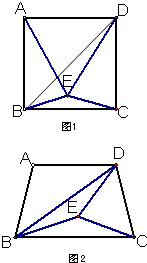 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.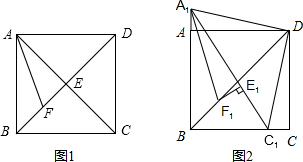 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.