Question

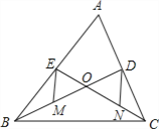
【题目】在数学活动课中，同学们准备了一些等腰直角三角形纸片，从每张纸片中剪出一个扇形制作圆锥玩具模型．如图，已知△ABC是腰长为4的等腰直角三角形．
（1）在等腰直角三角形ABC纸片中，以C为圆心，剪出一个面积最大的扇形（要求：尺规作图，保留作图痕迹，不写作法）；
（2）请求出所制作圆锥底面的半径长．

Answer 1

【答案】
（1）解：如图所示：扇形CEF为所求作的图形；

（2）解：∵△ABC是等腰直角三角形，且AC=BC=4，

∴AB= ，

由（1）可知CD平分∠ACB，

∴CD⊥AB，

∴CD= ，

设圆锥底面的半径长为r，依题意得：2πr= ，

∴r= ，

答：所制作圆锥底面的半径长为

【解析】（1）根据题意作出图形即可；（2根据勾股定理得到AB= ，由（1）可知CD平分∠ACB，根据等腰三角形的性质得到CD⊥AB，根据弧长的公式即可得到结论．
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)，还要掌握扇形面积计算公式(在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）)的相关知识才是答题的关键．