题目内容
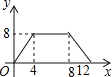
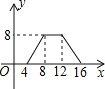
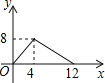
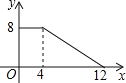
【题目】下图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120)。已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1) 当速度为50km/h、100km/h时,该汽车的耗油量分别为_____L/km、____L/km.
(2) 求线段AB所表示的y与x之间的函数表达式
(3) 速度是多少时,该汽车的耗油量最低?最低是多少?

【答案】(1)0.13,0.14.(2)y=-0.001x+0.18;(3)速度是80 km/h 时,该汽车的耗油量最低,最低是0.1 L / km.
【解析】(1)和(2):先求线段AB的解析式,因为速度为50km/h的点 在AB上,所以将x=50代入计算即可,速度是100km/h的点在线段BC上,可由已知中的“该汽车的速度每增加1km/h,耗油量增加0,002L/km”列式求得,也可以利用解析式求解;
(3)观察图形发现,两线段的交点即为最低点,因此求两函数解析式组成的方程组的解即可.
解:(1)设AB的解析式为:y=kx+b,
把(30,0.15)和(60,0.12)代入y=kx+b中得:
![]() ,解得
,解得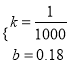 ,
,
∴AB:y=-0.001x+0.18,
当x=50时,y=-0.001×50+0.18=0.13,
由线段BC上一点坐标(90,0.12)得:0.12+(100-90)×0.002=0.14,
故答案为:0.13,0.14;
(2)设线段AB 所表示的y 与x 之间的函数表达式为y=kx+b.
因为y=kx+b 的图像过点(30,0.15)与(60,0.12),所以![]()
解方程组,得k=-0.001,b=0.18.
所以线段AB 所表示的y 与x 之间的函数表达式为y=-0.001x+0.18.
(3)根据题意,得线段BC 所表示的y 与x 之间的函数表达式为y=0.12+0.002(x-90)
=0.002x-0.06.
由图像可知,B 是折线ABC 的最低点.
解方程组![]() ,得
,得![]() .
.
因此,速度是80 km/h 时,该汽车的耗油量最低,最低是0.1 L / km.
“点睛”本题考查了一次函数的应用,正确求出两线段的解析式是解好本题的关键,因为系数为小数,计算要格外细心。容易出错,另外,此题中求最值的方法:两图象的交点,方程组的解;同时还有机地把函数和方程结合起来,是数学解题方法之一,应该熟练掌握.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】观察表格,结合其内容中所蕴含的规律和相关知识可知b=__________;
列举 | 猜想与发现 |
3,4,5 | 32=4+5 |
5,12,13 | 52=12+13 |
7,24,25 | 72=24+25 |
… | … |
17,b,c | 172=b+c |
【题目】A.B两地果园分别有苹果20吨和30吨,C.D两地分别需要苹果15吨和35吨;已知从A.B到C.D的运价如下表:
到C地 | 到D地 | |
A果园 | 每吨15元 | 每吨12元 |
B果园 | 每吨10元 | 每吨9元 |
(1)若从A果园运到C地的苹果为x吨,则从A果园运到D地的苹果为 吨,从A果园将苹果运往D地的运输费用为 元。
(2)用含x的式子表示出总运输费。(结果要化简)