题目内容
已知:梯形ABCD中,AD//BC,∠ABC=90。,AD=12,BC=18,AB=a,在线段BC上任取一点P,连结DP,作射线PE⊥DP,PE与直线AB交于点E。
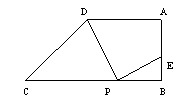
(1)确定CP=6时,点E的位置;
(2)若设CP=x,BE=y,求y关于x的函数关系式;
(3)若在线段BC上能找到不同的两个点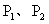 ,使上述作法得到的点E都与点A重合,求:a的取值范围。
,使上述作法得到的点E都与点A重合,求:a的取值范围。
(2)若设CP=x,BE=y,求y关于x的函数关系式;
(3)若在线段BC上能找到不同的两个点
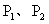 ,使上述作法得到的点E都与点A重合,求:a的取值范围。
,使上述作法得到的点E都与点A重合,求:a的取值范围。 (1)点E与B重合。
∵PB=BC-CP=18-6=12,
∴PB=AD=12,
又∵AD//BC,
∴四边形ABPD是平行四边形 ∵
∴平行四边形ABPD是知形
∴∠DPB=90。 ∴DP⊥BC
∵PE⊥DP 又 ∵点E在AB上
∴点E与B重合;
(2)作DF⊥BC,F为垂足,∵∠DPE=90。 ∴∠DPF+∠EPB =90。
∵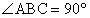 ∴∠EPB+∠PEB =90。 ∴∠DPF=∠PEB,
∴∠EPB+∠PEB =90。 ∴∠DPF=∠PEB,
∵∠DFP=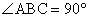
∴△DFP≌△PBE ∴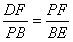
①当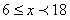 时 PF=x-6 ∴
时 PF=x-6 ∴ 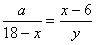
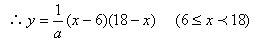
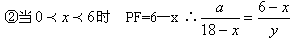
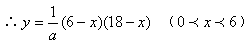
(3)由(2)得, ∵△DFP≌△PBE ∴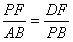
∴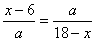 ∴
∴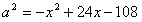
∴
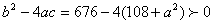
∴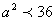 ∴a<6 ∵a>0 ∴0 <a<6
∴a<6 ∵a>0 ∴0 <a<6
∵PB=BC-CP=18-6=12,
∴PB=AD=12,
又∵AD//BC,
∴四边形ABPD是平行四边形 ∵
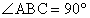
∴平行四边形ABPD是知形
∴∠DPB=90。 ∴DP⊥BC
∵PE⊥DP 又 ∵点E在AB上
∴点E与B重合;
(2)作DF⊥BC,F为垂足,∵∠DPE=90。 ∴∠DPF+∠EPB =90。
∵
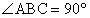 ∴∠EPB+∠PEB =90。 ∴∠DPF=∠PEB,
∴∠EPB+∠PEB =90。 ∴∠DPF=∠PEB,∵∠DFP=
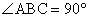
∴△DFP≌△PBE ∴
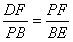
①当
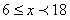 时 PF=x-6 ∴
时 PF=x-6 ∴ 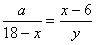
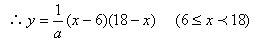
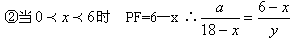
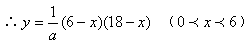
(3)由(2)得, ∵△DFP≌△PBE ∴
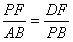
∴
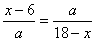 ∴
∴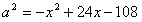
∴

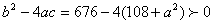
∴
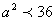 ∴a<6 ∵a>0 ∴0 <a<6
∴a<6 ∵a>0 ∴0 <a<6 
练习册系列答案
相关题目
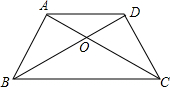 如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.
如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.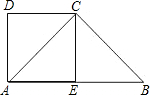 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=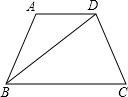 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=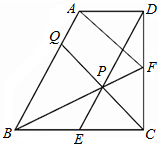 11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )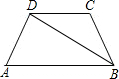 如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )
如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )