题目内容
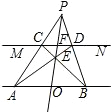在一次数学活动课上，一位同学提出：“谁能帮我用一副没有刻度的三角板找出线段AB的中点”小华说：“我能做到．我的做法是，用这副三角板任作一条直线MN∥AB；在直线AB、MN的同一侧任取一点P，连接PA、PB，分别交直线MN于C、D；再连接AD、BC，相交于点E；画射线PE交线段AB于点O，点O就是线段AB的中点．”你认为点O是线段AB的中点吗？并说明理由．
分析：由于CN∥AB，根据平行线分线段成比例可求出
=
，再根据△FDE∽△AOE，即可求出结论．
| FD |
| OB |
| CD |
| AB |
解答：解：∵CN∥AB，
∴
=
，
=
∴
=
又∵
=
∴
=
又∵△FDE∽△AOE
∴
=
∴
=
∴OB=AO．
∴
| FD |
| OB |
| PD |
| PB |
| CD |
| AB |
| PD |
| PB |
∴
| FD |
| OB |
| CD |
| AB |
又∵
| CD |
| AB |
| FE |
| EO |
∴
| FD |
| OB |
| FE |
| EO |
又∵△FDE∽△AOE
∴
| FD |
| AO |
| FE |
| ED |
∴
| FD |
| OB |
| FD |
| AO |
∴OB=AO．
点评：本题貌似复杂，实质上考查的是平行线分线段成比例定理及相似三角形的性质，是中学阶段的常规题．
练习册系列答案
相关题目
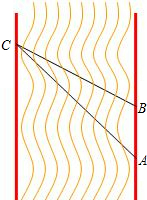在一次数学活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得C在A北偏西31°的方向上，沿河岸向北前行20米到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，帮助该同学计算出这条河的宽度．（参考数值：tan31°≈
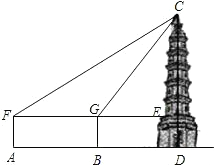时测得仰角∠CGE=37°，已知测倾器高1.5米，请你根据以上数据计算出古塔CD的高度．
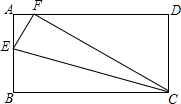在一次数学活动课上，张明同学将矩形ABCD沿直线CE折叠，顶点B恰好落在AD边上F点处，如图所示，已知CD=8cm，BE=5cm，则AD=
在一次数学活动课上，老师带领学生去测长江的宽度，某学生在长江北岸点A处观测到长江对岸水边有一点C，测得C在A东南方向上，沿长江边向东前行200米到达B处，测得C在B南偏东30°的方向上．
在一次数学活动课上，王老师给学生发了一块长40cm，宽30cm的长方形纸片（如图），要求折成一个高为5cm的无盖的且容积最大的长方体盒子．