题目内容
正 边形的每一个外角都是900;如果一个正多边形的每一个内角都是与它相邻外角的3倍,那么这个正多边形的内角和是 。
4,10800
多边形的外角和是360度,因为是正多边形,所以每一个外角都是90°,即可得到外角的个数,从而确定多边形的边数;
先设出外角的度数,利用外角与相邻内角和为180°列方程,解方程求出外角度数,再用360°÷这个外角度数,所得结果是多边形的边数,然后根据n边形内角和定理即可求出这个正多边形的内角和。
360÷90=4,所以这个正多边形是正四边形.
即正四边形的每一个外角都是90°;
设正多边形的每个外角为x°,则每个内角为3x°,
∴x+3x=180,
解得x=45.
∴多边形的边数为360°÷45°=8,
∴这个正八边形的内角和是(8-2)×180°=1080°.
故答案为4,1080°。
先设出外角的度数,利用外角与相邻内角和为180°列方程,解方程求出外角度数,再用360°÷这个外角度数,所得结果是多边形的边数,然后根据n边形内角和定理即可求出这个正多边形的内角和。
360÷90=4,所以这个正多边形是正四边形.
即正四边形的每一个外角都是90°;
设正多边形的每个外角为x°,则每个内角为3x°,
∴x+3x=180,
解得x=45.
∴多边形的边数为360°÷45°=8,
∴这个正八边形的内角和是(8-2)×180°=1080°.
故答案为4,1080°。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
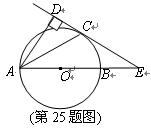
 A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.

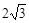 ,则∠BCD=________度.
,则∠BCD=________度.
 ,AB=3,弦BC∥OA,则劣弧BC的弧长为( )
,AB=3,弦BC∥OA,则劣弧BC的弧长为( )