题目内容
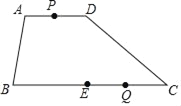
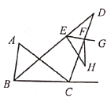
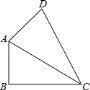
【题目】如图,![]() 是四边形
是四边形![]() 的对角线,
的对角线,![]() ,
,![]() ,
,![]() ,若
,若![]() ,则边
,则边![]() 的长为________.
的长为________.
【答案】![]()
【解析】
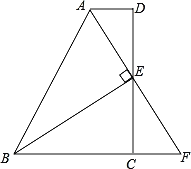
过点D作DE⊥BA的延长线于点E,连接EC交AD于点O,根据已知条件:AC=CD、∠ADC=∠ACB+45°,得∠CAD=∠ADC=∠ACB+45°;再根据∠BAC=90°-∠ACB,可推出∠EAD=45°,进而可得EA=ED,则有△EAC≌△EDC(SSS),∠AEO=∠DEO=45°,据此可得BE=BC;接下来根据BC=AB+![]() ,得到EB=AB+
,得到EB=AB+![]() ,故AE=
,故AE=![]() ,在Rt△AED中即可求解AD值.
,在Rt△AED中即可求解AD值.
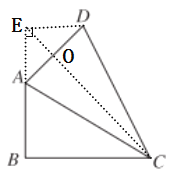
如图所示,过点D作DE垂直BA的延长线于点E,连接EC交AD于点O,
∵∠B=90°,
∴∠BAC=90°-∠ACB.
∵AC=CD,
∴∠CAD=∠ADC,
∵∠ADC=∠ACB+45°,
∴∠CAD=∠ACB+45°
∴∠BAD=135°,
∴∠EAD=45°,
∴EA=ED.
又∵AC=DC,EC=EC,
∴△EAC≌△EDC(SSS),
∴∠AEO=∠DEO=45°,
∴EB=BC=AB+![]() ,
,
∴AE=![]() .
.
∴在Rt△AED中,AD=![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目