题目内容
【题目】（1）如图1，已知△ABC，BF平分外角∠CBP，CF平分外角∠BCQ．试确定∠A和∠F的数量关系；
（2）如图2，已知△ABC，BF和BD三等分外角∠CBP，CF和CE三等分外角∠BCQ．试确定∠A和∠F的数量关系；
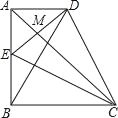
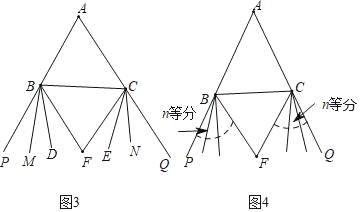
（3）如图3，已知△ABC，BF、BD和BM四等分外角∠CBP，CF、CE和CN四等分外角∠BCQ．试确定∠A和∠F的数量关系；
（4）如图4，已知△ABC，将外角∠CBP进行n等分，BF是临近BC边的等分线，将外角∠BCQ进行n等分，CF是临近BC边的等分线，试确定∠A和∠F的数量关系．
【答案】（1）∠F=90°-
∠A，理由见解析；（2）∠F=120°-
∠A，理由见解析；（3） ∠F=135°-
∠A，理由见解析；（4）∠F=
-
∠A，理由见解析.
【解析】
（1）利用三角形的外角的性质，角平分线的定义即可解决问题．
（2）利用三角形的外角的性质，三等分角的定义即可解决问题．
（3）利用三角形的外角的性质，四等分角的定义即可解决问题．
（4）利用三角形的外角的性质，n等分角的定义即可解决问题．
（1）由已知得∠CBF=∠CBP，∠BCF=∠BCQ，
∵∠CBP＝∠A+∠ACB，∠BCQ＝∠A+∠ABC，
∴∠CBF+∠BCF=(∠A+∠ACB+∠A+ABC)=(∠A+1800)，
∠F=1800-(∠CBF+∠BCF)=1800-(∠A+1800)= 90°-∠A；
（2）由已知得∠CBF=∠CBP，∠BCF=∠BCQ，
∵∠CBP＝∠A+∠ACB，∠BCQ＝∠A+∠ABC，
∴∠CBF+∠BCF=(∠A+∠ACB+∠A+ABC)=(∠A+1800)，
∠F=1800-(∠CBF+∠BCF)=1800-(∠A+1800)= 120°-∠A；
（3）由已知得∠CBF=∠CBP，∠BCF=∠BCQ，
∵∠CBP＝∠A+∠ACB，∠BCQ＝∠A+∠ABC，
∴∠CBF+∠BCF=(∠A+∠ACB+∠A+ABC)=(∠A+1800)，
∠F=1800-(∠CBF+∠BCF)=1800-(∠A+1800)= 135°-∠A；
（4）由已知得∠CBF=∠CBP，∠BCF=∠BCQ，
∴∠CBP＝∠A+∠ACB，∠BCQ＝∠A+∠ABC，
∴∠CBF+∠BCF=(∠A+∠ACB+∠A+ABC)=(∠A+1800)，
∠F=1800-(∠CBF+∠BCF)=1800-(∠A+1800)=
180°-∠A．
