题目内容
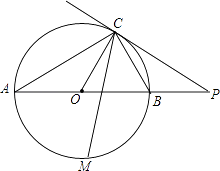
【题目】在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.
(1)当t为何值时,FC与EG互相平分;
(2)连接FG,当t< ![]() 时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
(3)设△EFG的面积为y,求出y与t的函数关系式,求当t为何值时,y有最大值?最大值是多少?
【答案】
(1)解:如图1,
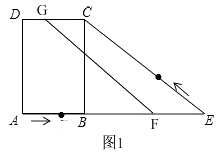
∵AB=4,∴BE=2AB=8,
在Rt△BCE中,根据勾股定理得,CE=10,
由运动知,CG=3t﹣10,EF=AB+BE﹣2t=12﹣2t.
∵FC与EG互相平分,
∴点G必在CD边上,
∴四边形CEFG是平行四边形,
∴CG=EF,
∴3t﹣10=12﹣2t,
∴t= ![]() ;
;
(2)解:∵当t< ![]() 时,点G在CE上,
时,点G在CE上,
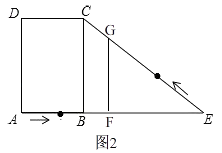
∵△EFG与△EBC相似,
当△EFG∽△EBC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
当△EGF∽△EBC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ;
;
(3)解:当点G在CE上时,即:0<t≤ ![]() ,如图3,
,如图3,
过点G作GM⊥BE,
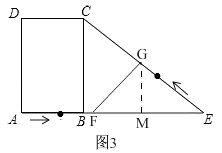
∴GM∥BC,
∴△EMG∽△EBC,
∴ ![]() ,
,
∴ ![]() ,
,
∴GM= ![]() t,
t,
∴y=S△EFG= ![]() EFGM=
EFGM= ![]() ×(12﹣2t)×
×(12﹣2t)× ![]() t=﹣
t=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣3)2+
(t﹣3)2+ ![]() ;
;
当t=3时,y最大= ![]() .
.
当点G在CD上时,即: ![]() <t≤
<t≤ ![]() ,
,
y=S△EFG= ![]() EF×BC=
EF×BC= ![]() (12﹣2t)×6=﹣6t+36.
(12﹣2t)×6=﹣6t+36.
即:t=3时,y最大= ![]() .
.
【解析】(1)在Rt△BCE中,根据勾股定理得,由运动知,CG=3t﹣10,EF=AB+BE﹣2t=12﹣2t.CE=10,判断出四边形CEFG是平行四边形,再用对边相等建立方程即可得出结论;(2)分当t< ![]() 时,点G在CE上与当点G在CD上时,即:
时,点G在CE上与当点G在CD上时,即: ![]() <t≤
<t≤ ![]() 两种情况,用相似三角形的对应边成比例建立方程即可;(3)分点G在CE上时,即:0<t≤
两种情况,用相似三角形的对应边成比例建立方程即可;(3)分点G在CE上时,即:0<t≤ ![]() 与点G在CD上时,即:
与点G在CD上时,即: ![]() <t≤
<t≤![]() 两种情况,用三角形的面积y=S△EFG=
两种情况,用三角形的面积y=S△EFG= ![]() EFGM与y=S△EFG=
EFGM与y=S△EFG= ![]() EF×BC即可。
EF×BC即可。
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

【题目】某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题:
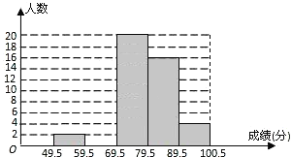
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 |
| 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 |
| 1 |
(1)频数、频率分布表中![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是多少?