Question

【题目】如图，抛物线y=﹣x2+3x+4与x轴交于点A，B，与y轴交于点C，P（m，n）为第一象限内抛物线上的一点，点D的坐标为（0，6）．

（1）OB=_________，抛物线的顶点坐标为_________________；

（2）当n=4时，求点P关于直线BC的对称点P′的坐标；

（3）是否存在直线PD，使直线PD所对应的一次函数随x的增大而增大？若存在，直接写出m的取值范围；若不存在，请说明理由．

Answer 1

【答案】（1）4，（，）；（2）（0，1）；（3）1＜m＜2．

【解析】

试题分析：（1）当y=0时，即﹣x2+3x+4=0，解得：x1=4，x2=﹣1，∴点A（﹣1，0）点B（4，0），∴OB=4，y=﹣x2+3x+4=，∴抛物线的顶点坐标为（，），故答案为：4，（，）．

（2）如图，连接CP，CP′，

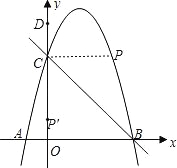
n=4时，﹣m2+3m+4=4，解得：m1=3，m2=0（舍去），∴这时P点的坐标为（3，4），∵OC=4，∴CP∥x轴，CP=3，∵点C的坐标为（0，4），∴OB=OC=4，∴∠OCB=45°=∠BCP，∴点P′在y轴上，且CP′=CP=3，∴P′的坐标为（0，1）．

（3）存在，∵点D的坐标为（0，6），∴当y=6时，﹣x2+3x+4=6，解得：x1=1，x2=2，∵直线PD所对应的一次函数随x的增大而增大，∴一次函数的图象一定经过一、三象限，∴1＜m＜2．