Question

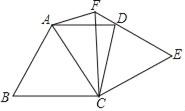
【题目】如图，将等边△ABC绕点C顺时针旋转90°得到△EFC，∠ACE的平分线CD交EF于点D，连接AD、AF．

（1）求∠CFA度数；

（2）求证：AD∥BC．

Answer 1

【答案】（1）75°（2）见解析

【解析】

（1）由等边三角形的性质可得∠ACB＝60°，BC＝AC，由旋转的性质可得CF＝BC，∠BCF＝90°，由等腰三角形的性质可求解；

（2）由“SAS”可证△ECD≌△ACD，可得∠DAC＝∠E＝60°＝∠ACB，即可证AD∥BC．

解：（1）∵△ABC是等边三角形

∴∠ACB＝60°，BC＝AC

∵等边△ABC绕点C顺时针旋转90°得到△EFC

∴CF＝BC，∠BCF＝90°，AC＝CE

∴CF＝AC

∵∠BCF＝90°，∠ACB＝60°

∴∠ACF＝∠BCF﹣∠ACB＝30°

∴∠CFA＝（180°﹣∠ACF）＝75°

（2）∵△ABC和△EFC是等边三角形

∴∠ACB＝60°，∠E＝60°

∵CD平分∠ACE

∴∠ACD＝∠ECD

∵∠ACD＝∠ECD，CD＝CD，CA＝CE，

∴△ECD≌△ACD（SAS）

∴∠DAC＝∠E＝60°

∴∠DAC＝∠ACB

∴AD∥BC