题目内容
如图甲,在正方形ABCD的边上有一个动点P以2cm/s的速度,从点B开始按B-C-D-A运动,到点A为止.设点P移动时间为t,△ABP的面积为S. S关于t的函数关系如图乙所示,回答下列问题: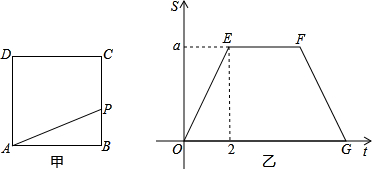 (1)图甲中的BC长是多少?
(1)图甲中的BC长是多少?(2)图乙中的a是多少?
(3)当t为什么值时,S=2cm2.
分析:(1)由图甲、乙可知,从B点
C点所经过的时间为2s,那么所经过的路程=速度×时间,即为BC的长;
(2)根据题目说明及图甲、乙,甲图中C点对应乙图中E点,甲图中的D点对应乙图中的F,即乙图中的EF段反映了P点从C点
D点,由图中可看出a实际就是△APB的面积;
(3)观察图甲可知,当P运动在BC段、AD段时,S有可能等于2cm2,因而分这两种情况讨论.
| 移动 |
(2)根据题目说明及图甲、乙,甲图中C点对应乙图中E点,甲图中的D点对应乙图中的F,即乙图中的EF段反映了P点从C点
| 移动 |
(3)观察图甲可知,当P运动在BC段、AD段时,S有可能等于2cm2,因而分这两种情况讨论.
解答:解:(1)由图甲、乙知,从B点→C点所经过的时间为2s
从B点→C点所经过的路程为2×2=4cm
∴BC的长是4m
(2)由图甲、乙得
a=S△APB=
AB•BC=
×4×4=8
(3)当P点从B点
C点时,BP=2t
则S△APB=
AB•BP=
×4×2t=2,解得t=0.5(s)
当P点从D点
A点时,AP=(BC+CD+AD)-(BC+CD+DP)=12-2t
则S△APB=
AB•AP=
×4×(12-2t)=2,解得t=5.5(s)
答:(1)图甲中的BC长是4cm;(2)图乙中的a是8cm2;(3)当t为0.5s或5.5s时,S=2cm2.
从B点→C点所经过的路程为2×2=4cm
∴BC的长是4m
(2)由图甲、乙得
a=S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
(3)当P点从B点
| 移动 |
则S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
当P点从D点
| 移动 |
则S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)图甲中的BC长是4cm;(2)图乙中的a是8cm2;(3)当t为0.5s或5.5s时,S=2cm2.
点评:本题考查一次函数的应用.解决本题的关键是读懂图甲与图乙的对应关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

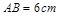 ,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题: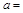 ;
;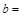 ;
;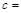 .
.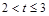 时,求S与t的函数关系式;
时,求S与t的函数关系式;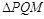 能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.
能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.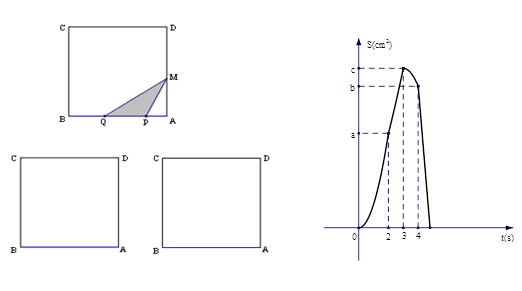
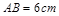 ,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题: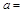 ;
;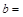 ;
;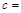 .
.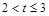 时,求S与t的函数关系式;
时,求S与t的函数关系式; 能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.
能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.