题目内容
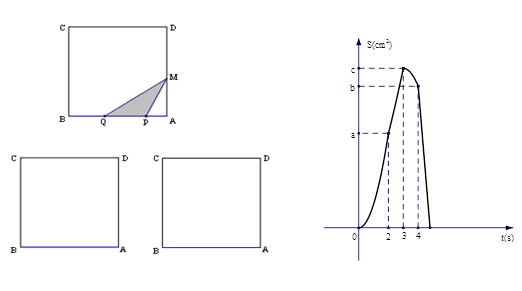
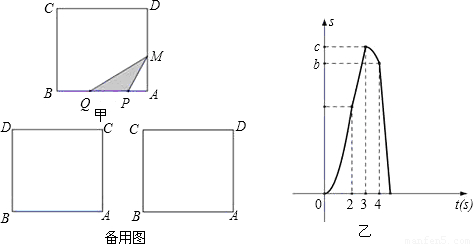
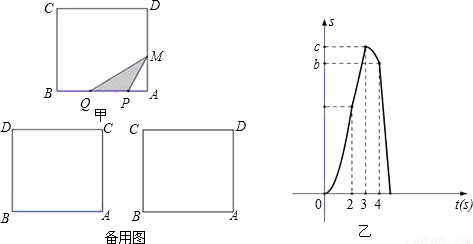
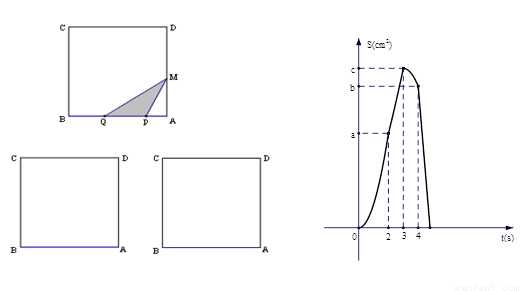
如图甲,在正方形ABCD中,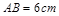 ,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
(1)当t为何值时,点M与点Q相遇?
(2)填空: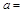 ;
;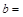 ;
;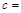 .
.
(3)当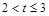 时,求S与t的函数关系式;
时,求S与t的函数关系式;
(4)在整个运动过程中,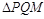 能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.
能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.
解:⑴ 根据题意可列方程为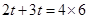 ,则
,则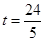
答:当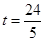 时,点M与点Q相遇。---------------------------------3分
时,点M与点Q相遇。---------------------------------3分
⑵ 8;13.5;12(每空1分)
(3)当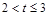 时,
时,
S与t的函数关系式是
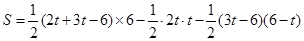
=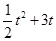 -----------------------------------------------------------------------------------9分
-----------------------------------------------------------------------------------9分
(4) 当0<t≤2时,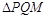 不能成为直角三角形;
不能成为直角三角形;
当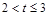 时,若能成为直角三角形,则有△BPQ∽△CMP,即
时,若能成为直角三角形,则有△BPQ∽△CMP,即
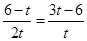 ,可求出
,可求出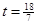 ;
;
当3<t≤4时,若能成为直角三角形,则有△BPQ∽△AQM,即
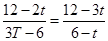 ,无解;
,无解;
当4<t<4.8时,
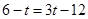 ,
,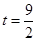 ----------------------------------------------------------------12分
----------------------------------------------------------------12分
【解析】(1)根据题意列出方程2t+3t=4×6求解即可;
(2)分别令时间t为2、3、4求得相应的三角形的面积即为a、b、cd的值;
(3)当2<t≤3时即点P、Q在线段AB上运动时,表示出该三角形的面积即可;
(4)分0<t≤2、2<t≤3、2<t≤3、4<t<4.8四种情况讨论.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
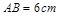 ,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题: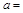 ;
;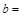 ;
;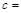 .
.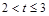 时,求S与t的函数关系式;
时,求S与t的函数关系式;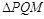 能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.
能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.