题目内容
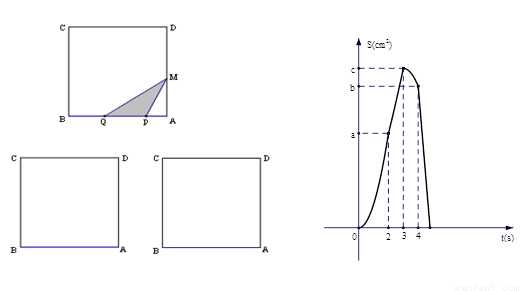
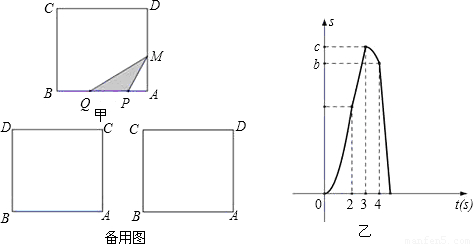
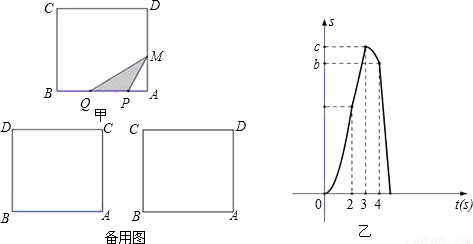
如图甲,在正方形ABCD中,AB=6cm,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s,点M的速度2cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm
2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
(1)当t为何值时,点M与点Q相遇?
(2)填空:a=
;b=
;c=
.
(3)当2<t≤3时,求S与t的函数关系式;
(4)在整个运动过程中,△PQM能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.

分析:(1)根据题意列出方程2t+3t=4×6求解即可;
(2)分别令时间t为2、3、4求得相应的三角形的面积即为a、b、cd的值;
(3)当2<t≤3时即点P、Q在线段AB上运动时,表示出该三角形的面积即可;
(4)分0<t≤2、2<t≤3、2<t≤3、4<t<4.8四种情况讨论.
解答:解:(1)根据题意可列方程为2t+3t=4×6,则
t=答:当
t=时,点M与点Q相遇.
(2)8;12;13.5;
(3)当2<t≤3时,
S与t的函数关系式是
S=(2t+3t-6)×6-•2t•t-(3t-6)(6-t)=
t2+3t;
(4)当0<t≤2时,△PQM不能成为直角三角形;
当2<t≤3时,若能成为直角三角形,则有△BPQ∽△CMP,即
=,可求出
t=;
当3<t≤4时,若能成为直角三角形,则有△BPQ∽△AQM,即
=,无解;
当4<t<4.8时,6-t=3t-12,
t=.
点评:本题考查了动点问题,是难点,也是中考的重点,需熟练掌握.
练习册系列答案
相关题目


 名校课堂系列答案
名校课堂系列答案 ,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题: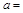 ;
;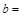 ;
;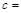 .
.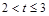 时,求S与t的函数关系式;
时,求S与t的函数关系式;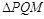 能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.
能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.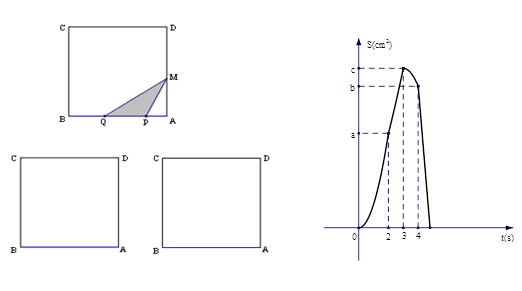
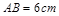 ,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题:
,点P、Q从A点沿边AB、BC、CD运动,点M从A点沿边AD、DC、CB运动,点P、Q的速度分别为1cm/s,3cm/s ,点M的速度2 cm/s.若它们同时出发,当点M与点Q相遇时,所有点都停止运动.设运动的时间为ts,△PQM的面积为Scm2,则S关于t的函数图象如图乙所示.结合图形,完成以下各题: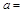 ;
;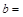 ;
;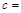 .
.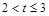 时,求S与t的函数关系式;
时,求S与t的函数关系式;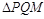 能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.
能否为直角三角形?若能,请求出此时t的值;若不能,请说明理由.