题目内容
【题目】填写推理理由：
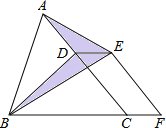
已知：如图，D，F，E分别是BC，AC，AB上的点，DF∥AB，DE∥AC，试说明∠EDF＝∠A.
解：∵DF∥AB ( )，
∴∠A＋∠AFD＝180° ( )．
∵DE∥AC ( )，
∴∠AFD＋∠EDF＝180° ( )．
∴∠A＝∠EDF ( )．
【答案】两直线平行，同旁内角互补；已知；两直线平行，同旁内角互补；同角的补角相等.
【解析】试题分析：DF∥AB是已知条件，理由填已知；由DF∥AB得到∠A＋∠AFD＝180°，理由是两直线平行，同旁内角互补；DE∥AC是已知条件，理由填已知；由DE∥AC得到∠AFD＋∠EDF＝180°，理由是两直线平行，同旁内角互补；再根据同角的补角相等即可得∠A＝∠EDF.
试题解析：
∵DF∥AB(已知)，
∴∠A＋∠AFD＝180°(两直线平行，同旁内角互补)．
∵DE∥AC(已知)，
∴∠AFD＋∠EDF＝180°(两直线平行，同旁内角互补)．
∴∠A＝∠EDF(同角的补角相等)．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
