题目内容
【题目】如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．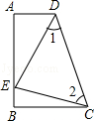 
（1）求证：Rt△ADE与Rt△BEC全等；
（2）求证：△CDE是直角三角形．
【答案】
（1）解：全等．理由是：
∵∠1=∠2，
∴DE=CE，
∵∠A=∠B=90°，AE=BC，
在Rt△ADE和Rt△BEC中，
，
∴Rt△ADE≌Rt△BEC（HL）．
（2）解：是直角三角形．理由是：
∵Rt△ADE≌Rt△BEC，
∴∠AED=∠BCE，
∵∠ECB+∠BEC=90°，
∴∠AED+∠BEC=90°．
∴∠DEC=90°，
∴△CDE是直角三角形．
【解析】（1）估计等边对等角，推出DE=EC，再根据HL即可证明Rt△ADE≌Rt△BEC；（2）由Rt△ADE≌Rt△BEC，推出∠AED=∠BCE，由∠ECB+∠BEC=90°，推出∠AED+∠BEC=90°．即∠DEC=90°；
练习册系列答案
相关题目
