题目内容
(10分)已知:如图,在梯形ABCD中,AD∥BC,∠DCB = 90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为![]() ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
①当![]() = 1时,是 ;
= 1时,是 ;
②当![]() = 2时,是 ;
= 2时,是 ;
③当![]() = 3时,是 .
= 3时,是 .
请证明![]() = 2时的结论.
= 2时的结论.
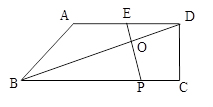

(1)证明:∵AD∥BC
∴∠OBP = ∠ODE ……………1分
在△BOP和△DOE中
∠OBP = ∠ODE
∠BOP = ∠DOE …………………2分
∴△BOP∽△DOE (有两个角对应相等的两三角形相似) ……………3分
(2)① 平行四边形 …………………4分
② 直角梯形 …………………5分
③ 等腰梯形 …………………7分
证明:∵k = 2时, ![]()
∴ BP = 2DE= AD
又∵AD︰BC = 2︰3 BC = ![]() AD
AD
PC = BC- BP =![]() AD- AD =
AD- AD =![]() AD= ED
AD= ED
ED∥PC , ∴四边形PCDE是平行四边形
∵∠DCB= 90°
∴四边形PCDE是矩形 …………………8分
∴ ∠EPB =90° …………………9分
又∵ 在直角梯形ABCD中
AD∥BC, AB与DC不平行
∴ AE∥BP, AB与EP不平行
四边形ABPE是直角梯形 ………………………10分
(本题其它证法参照此标准给分)
解析:略

 阅读快车系列答案
阅读快车系列答案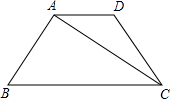 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.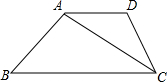 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,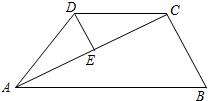 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=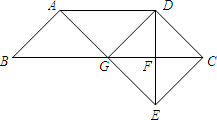 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.